题目内容
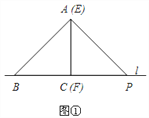
【题目】如图①,将两块全等的三角板拼在一起,其中△ABC的边BC在直线l上,AC⊥BC且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,EF⊥FP且EF=FP.
(1)在图①中,通过观察、测量,猜想直接写出AB与AP满足的数量关系和位置关系,不要说明理由;
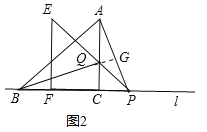
(2)将三角板△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP、BQ.猜想写出BQ与AP满足的数量关系和位置关系,并说明理由.
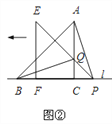
【答案】(1)AB=AP且AB⊥AP,(2)BQ与AP所满足的数量关系是AP=BQ,位置关系是AP⊥BQ
【解析】分析:(1)根据等腰直角三角形性质得出AB=AP,∠BAC=∠PAC=45°,求出∠BAP=90°即可;
(2)求出CQ=CP,根据SAS证△BCQ≌△ACP,推出AP=BQ,∠CBQ=∠PAC,根据三角形内角和定理求出∠CBQ+∠BQC=90°,推出∠PAC+∠AQG=90°,求出∠AGQ=90°即可.
详解:(1)AB=AP且AB⊥AP。理由如下:
∵AC⊥BC且AC=BC,∴△ABC为等腰直角三角形,
∴∠BAC=∠ABC=![]() (180°﹣∠ACB)=45°.
(180°﹣∠ACB)=45°.
又∵△ABC与△EFP全等,同理可证∠PEF=45°,
∴∠BAP=45°+45°=90°,∴AB=AP且AB⊥AP.
(2)BQ与AP所满足的数量关系是AP=BQ,位置关系是AP⊥BQ,理由如下:
延长BQ交AP于G,由(1)知,∠EPF=45°,∠ACP=90°,
∴∠PQC=45°=∠QPC,∴CQ=CP.
∵∠ACB=∠ACP=90°,AC=BC,∴在△BCQ和△ACP中,
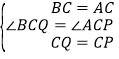 ,
,
∴△BCQ≌△ACP(SAS),
∴AP=BQ,∠CBQ=∠PAC.
∵∠ACB=90°,∴∠CBQ+∠BQC=90°.
∵∠CQB=∠AQG,∴∠AQG+∠PAC=90°,
∴∠AGQ=180°﹣90°=90°,∴AP⊥BQ.