题目内容
【题目】已知∠AOB及其内部一点P,试讨论以下问题的解答:
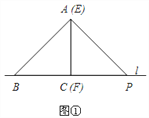
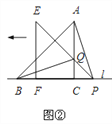
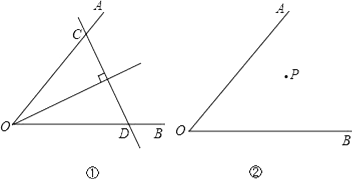
(1)如图①,若点P在∠AOB的平分线上,我们可以过P点作直线垂直于角平分线,分别交OA、OB于点C、D,则可以得到△OCD是以CD为底边的等腰三角形;若点P不在∠AOB的平分线上(如图②),你能过P点作直线,分别交OA、OB于点C、D,得到△OCD是等腰三角形,且CD是底边吗?请你在图②中画出图形,并简要说明画法.
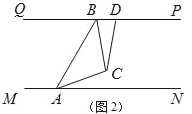
(2)若点P不在∠AOB的平分线上(如图③),我们可以过P点作PQ∥OA,并作∠QPR=∠AOB,直线PR分别交OA、OB于点C、D,则可以得到△OCD是以OC为底的等腰三角形.请你说明这样作的理由.
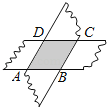
(3)若点P不在∠AOB的平分线上,请你利用在(2)中学到的方法,在图④中过P点作直线分别交OA、OB于点C、D,使得△OCD是等腰三角形,且OD是底边.保留画图的痕迹,不用写出画法.

【答案】(1)能,画法见解析;(2)理由见解析;(3)见解析.
【解析】试题分析:(1)作∠AOB的平分线,过P点作角平分线的垂线,分别交角的两边OA、OB于点C、D,则△OCD是以CD为底边的等腰三角形;
(2)根据PQ∥OA,得出∠QPR=∠OCD,进而得出OD=CD,即可得出答案;
(3)作QP∥DO,再作∠ODR=∠O,即可得出答案.
试题解析:解:(1)能.
画法:作∠AOB的平分线,过P点作角平分线的垂线,分别交角的两边OA、OB于点C、D,则△OCD是以CD为底边的等腰三角形,如图①.
(2)∵PQ∥OA,∴∠QPR=∠OCD.
又∵∠QPR=∠AOB,∴∠OCD=∠AOB,∴OD=CD.
即△OCD是以OC为底的等腰三角形.
(3)如图②.
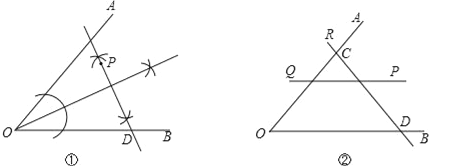

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目