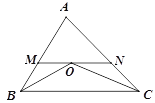
[题目]如图.△ABC中.BO平分∠ABC.CO平分∠ACB.MN经过点O.与AB.AC相交于点M.N.且MN∥BC.若AB=5.AC=6.则△AMN的周长为( )A. 7 B. 9 C. 11 D. 16 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，△ABC中，BO平分∠ABC，CO平分∠ACB，MN经过点O，与AB，AC相交于点M，N，且MN∥BC，若AB=5，AC=6，则△AMN的周长为（）

A. 7 B. 9 C. 11 D. 16

【答案】C

【解析】

由BO平分∠ABC可知∠MBO=∠CBO，再由MN∥BC可得∠MOB=∠CBO，则∠MOB=∠CBO=∠MBO，则MB=MO，同理可得NO=NC，则△AMN的周长为AM+MO+NO+AN=AB+AC.

解：∵BO平分∠ABC，CO平分∠BCO，

∴∠MBO=∠CBO，∠NCO=∠CBO，

∵MN∥BC，

∴∠MOB=∠CBO=∠MBO，∠NOC=∠BCO=∠NCO，

∴MB=MO，NO=NC，

∴△AMN的周长=AB+MN+AN=AM+MO+NO+AN=AB+AC=5+6=11,

故选择C.

练习册系列答案

【题目】已知∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F，AB =12，AC =6，则BE= ___________.

【题目】居民区内的广场舞引起了媒体关注，小明想了解本小区居民对广场舞的看法，进行了一次抽样调查，把居民对广场舞的看法分为低各层次：A．非常赞同；B．赞同但要有时间限制；C．无所谓；D．不赞同．并将调查结果绘制成了图1和图2两幅不完整的统计图．
请你根据图中的信息回答下列问题：
（1）求本次被抽查的居民有多少？
（2）将图1和图2补充完整；
（3）求图2中“C”层次所在扇形的圆心角度数；
（4）估计该小区4000名居民中对广场舞的看法表示赞同（包括A层次和B层次）的人数大约多少人．

【题目】保护环境、低碳出行已渐渐成为人们的习惯．最近无为县城又引进了共享单车，只需要交点押金，就可以通过扫描二维码的方式解锁一辆停在路边的自行车，以极低的费用，轻松骑到目的地．王老师家与学校相距2km，现在每天骑共享单车到学校所花的时间比过去骑电动车多用4min．已知王老师骑电动车的速度是骑共享单车速度的1.5倍，则王老师骑共享单车的速度是多少？

【题目】如图，已知A（1，6）B（n，﹣2）是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点，直线与y轴交于C点．
（1）求反比例函数和一次函数的表达式；
（2）求△BOC的面积；
（3）直接写出不等式kx+b﹣ ＞0的解集．

【题目】实验探究题
（1）操作发现：
在△ABC中，AB=AC，∠BAC=90°，D在线段BC上（不与点B重合），连接AD，将线段AD绕A点逆时针旋转90°得到AE，连接EC，如图①所示，请直接写出线段CE和BD的位置关系和数量关系．
（2）猜想论证：
在（1）的条件下，当D在线段BC的延长线上时，请你在图②中画出图形并判断（1）中的结论是否成立，并证明你的判断．

（3）拓展延伸：
如图③，若AB≠AC，∠BAC≠90°，点D在线段BC上运动，试探究：当锐角∠ACB等于度时，线段CE和BD之间的位置关系仍成立（点C、E重合除外）？此时若作DF⊥AD交线段CE于点F，且当AC=3 时，请直接写出线段CF的长的最大值是．

【题目】如图，在△OAB中，OA=OB，以点O为圆心的⊙O经过AB的中点C，直线AO与⊙O相交于点E、D，OB交⊙O于点F，P是的中点，连接CE、CF、BP．
（1）求证：AB是⊙O的切线．
（2）若OA=4，则 ①当长为时，四边形OECF是菱形；
②当长为时，四边形OCBP是正方形．

【题目】如图1，长方形OABC的边OA在数轴上，O为原点，长方形OABC的面积为12，OC边长为3.

(1)数轴上点A表示的数为________．

(2)将长方形OABC沿数轴水平移动，移动后的长方形记为O′A′B′C′，移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.

①当S恰好等于原长方形OABC面积的一半时，数轴上点A′表示的数是多少？

　 ②设点A的移动距离AA′＝x.

　（ⅰ)当S＝4时，求x的值；

　（ⅱ)D为线段AA′的中点，点E在线段OO′上，且OE＝OO′，当点D，E所表示的数互为相反数时，求x的值．

试题分类