��Ŀ����
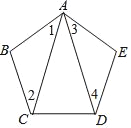
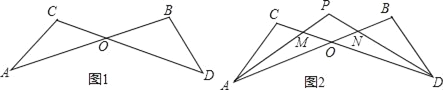
����Ŀ����ͼ1����֪�߶�AB��CD�ཻ�ڵ�O������AC��BD�������ǰ�����������ͼ�γ�Ϊ��8���͡���
(1)��֤����A+��C����B+D��
(2)��ͼ2������CAB�͡�BDC��ƽ����AP��DP�ཻ�ڵ�P������CD��AB�ֱ��ཻ�ڵ�M��N��
�����߶�ACΪ�ߵġ�8���͡����� �������Ե�OΪ����ġ�8���͡����� ������
������B��100�㣬��C��120�㣬���P�Ķ�����
������ƽ�����нǵĹ�ϵ��Ϊ����CAP��![]() ��CAB����CDP��
��CAB����CDP��![]() ��CDB������̽����P����B����C֮����ڵ�������ϵ����֤�����ɣ�
��CDB������̽����P����B����C֮����ڵ�������ϵ����֤�����ɣ�
���𰸡�(1)֤����������(2)��3�� 4������P��110�㣻��3��P����B+2��C�����ɼ�����.
��������
(1)���������ڽǺ͵õ���A+��C=180�㩁��AOC����B+��D=180�㩁��BOD���ɶԶ�����ȣ��õ���AOC=��BOD�������A+��C=��B+��D��
(2)�����߶�ACΪ�ߵġ�8���Ρ���3������OΪ����ġ�8���Ρ���4����
������(1)�Ľ�������MΪ������8�������У���P+��CDP����C+��CAP����NΪ������8�������У���P+��BAP����B+��BDP������ʽ��ӵõ�2��P+��BAP+��CDP=��B+��C+��CAP+��BDP����AP��DP�ǽ�ƽ���ߣ��õ���BAP����CAP����CDP����BDP���Ӷ���P=![]() (��B+��C)��Ȼ����B=100����C=120������㼴�ɣ�
(��B+��C)��Ȼ����B=100����C=120������㼴�ɣ�
����ڵ�֤������һ���õ�3��P=��B+2��C.
����(1)��ͼ1�У��С�A+��C��180�㩁��AOC����B+��D��180�㩁��BOD��
�ߡ�AOC����BOD��
���A+��C����B+��D��
(2)�⣺�����߶�ACΪ�ߵġ�8���͡���3����



�Ե�OΪ����ġ�8���͡���4����




����MΪ���㡰8���͡��У��С�P+��CDP����C+��CAP��
��NΪ���㡰8���͡��У��С�P+��BAP����B+��BDP
��2��P+��BAP+��CDP����B+��C+��CAP+��BDP��
��AP��DP�ֱ�ƽ�֡�CAB�͡�BDC��
���BAP����CAP����CDP����BDP��
��2��P����B+��C��
�ߡ�B��100�㣬��C��120�㣬
���P��![]() ����B+��C��=
����B+��C��=![]() ��100��+120�㣩��110�㣻
��100��+120�㣩��110�㣻
��3��P����B+2��C���������ǣ�
�ߡ�CAP��![]() ��CAB����CDP��
��CAB����CDP��![]() ��CDB��
��CDB��
���BAP��![]() ��CAB����BDP��
��CAB����BDP��![]() ��CDB��
��CDB��
��MΪ���㡰8���͡��У��С�P+��CDP����C+��CAP��
��NΪ���㡰8���͡��У��С�P+��BAP����B+��BDP
���C����P����CDP����CAP��![]() ����CDB����CAB����
����CDB����CAB����
��P����B����BDP����BAP��![]() ����CDB����CAB����
����CDB����CAB����
��2����C����P������P����B��
��3��P����B+2��C��
�ʴ�Ϊ��(1)֤����������(2)��3�� 4������P��110�㣻��3��P����B+2��C�����ɼ�����.