��Ŀ����
����Ŀ��Ϊ�˸��õ����ø�������ij���ί�����۾�������![]() �����ͺŵĿ��ֹ��༶ѧ��ʹ�ã���֪
�����ͺŵĿ��ֹ��༶ѧ��ʹ�ã���֪![]() �Ϳ���ÿ���۸�
�Ϳ���ÿ���۸�![]() Ԫ��
Ԫ��![]() �Ϳ���ÿ���۸��
�Ϳ���ÿ���۸��![]() ����4Ԫ��180ԪǮ�����
����4Ԫ��180ԪǮ�����![]() �Ϳ��ֱ�
�Ϳ��ֱ�![]() �Ϳ�����12����
�Ϳ�����12����
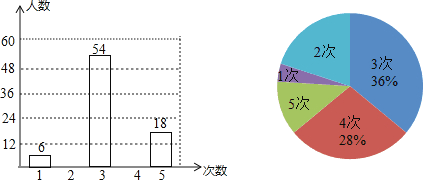
��1����![]() ��ֵ��
��ֵ��
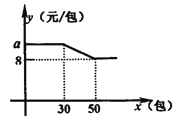
��2�������̼�Э�̣�����![]() �Ϳ��ּ۸�����Żݣ�����ÿ���۸�
�Ϳ��ּ۸�����Żݣ�����ÿ���۸�![]() ��Ԫ����������
��Ԫ����������![]() �������ĺ�����ϵ��ͼ��ʾ��
�������ĺ�����ϵ��ͼ��ʾ��![]() �Ϳ���һ�ɰ�ԭ�����ۣ�
�Ϳ���һ�ɰ�ԭ�����ۣ�
����![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
������ί��ƻ�����![]() �͡�
�͡�![]() ����100��������
����100��������![]() �Ͳ�����30�����Ҳ�����60�����ʹ���
�Ͳ�����30�����Ҳ�����60�����ʹ���![]() �Ϳ��ֶ��ٰ�ʱ��������ֵ��ܽ�����٣�����Ϊ����Ԫ��
�Ϳ��ֶ��ٰ�ʱ��������ֵ��ܽ�����٣�����Ϊ����Ԫ��
���𰸡���1��![]() ����2���ٵ�
����2���ٵ�![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ���ڵ�����
���ڵ�����![]() �Ϳ���50��ʱ��������ֵ��ܽ�����٣�����Ϊ700Ԫ
�Ϳ���50��ʱ��������ֵ��ܽ�����٣�����Ϊ700Ԫ
��������
��1�����ܼ���ÿ������=���������ݡ�180ԪǮ�����![]() �Ϳ��ֱ�
�Ϳ��ֱ�![]() �Ϳ�����12�������з�ʽ���̼�����⣻
�Ϳ�����12�������з�ʽ���̼�����⣻
��2����ͼ����Ϣ�ɵú�����ϵ�����е�![]() ʱ��
ʱ��![]() ��
��![]() ֮������һ�κ�����ϵ���ɴ���ϵ����������⣬
֮������һ�κ�����ϵ���ɴ���ϵ����������⣬
��3����![]() �Ϳ��ֹ���
�Ϳ��ֹ���![]() ����������������ۣ���
����������������ۣ���![]() ��
��![]() ʱ�����������ֵ��ܽ����
ʱ�����������ֵ��ܽ����![]() �Ϳ��ְ����ĺ�����ϵ�������ú�����������⣮
�Ϳ��ְ����ĺ�����ϵ�������ú�����������⣮
�⣺��1����������ɵã�![]() ��
��
���![]() ��
��![]() ��������
��������![]() ��
��![]() ��ԭ���̵Ľ⣬
��ԭ���̵Ľ⣬
��![]() ���������⣬��ȥ��
���������⣬��ȥ��
��![]() ��
��
��2��������ͼ����Ϣ�ã�
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��![]() ֮������һ�κ�����ϵ��
֮������һ�κ�����ϵ��
�躯������ʽΪ![]() ��ȡ��
��ȡ��![]() ��
��![]()
�����![]() �����
�����![]() ��
��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
������������![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��
����![]() �Ϳ��ֹ���
�Ϳ��ֹ���![]() ������
������![]() �Ϳ���Ϊ
�Ϳ���Ϊ![]() �����������ֿ��ֵ��ܽ��Ϊ
�����������ֿ��ֵ��ܽ��Ϊ![]() Ԫ��
Ԫ��
��������![]() ��
��![]()
![]() ��
��
��![]() ʱ��
ʱ��![]() ȡ���ֵ722.5��
ȡ���ֵ722.5��
��![]() ʱ��
ʱ��![]() ȡ��Сֵ700Ԫ��
ȡ��Сֵ700Ԫ��
����![]() ʱ��
ʱ��![]() ��
��
��������![]() ʱ��������ã�
ʱ��������ã�![]() ��
��![]() ��
��![]() �����������
�����������
��![]() ��
��
���ϣ�������![]() �Ϳ���50��ʱ��������ֵ��ܽ�����٣�����Ϊ700Ԫ��
�Ϳ���50��ʱ��������ֵ��ܽ�����٣�����Ϊ700Ԫ��