Question

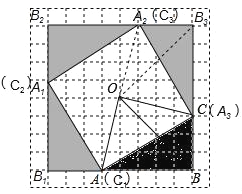
【题目】如图，在网格中有一个四边形图案．

（1）请你分别画出△ABC绕点O顺时针旋转90°的图形，关于点O对称的图形以及逆时针旋转90°的图形，并将它们涂黑；

（2）若网格中每个小正方形的边长为1，旋转后点A的对应点依次为A1，A2，A3，求四边形AA1A2A3的面积；

（3）这个美丽图案能够说明一个著名结论的正确性，请写出这个结论．

Answer 1

【答案】(1)详见解析；（2）34；（3）勾股定理．

【解析】

试题分析：（1）根据图形旋转的性质画出旋转后的三角形即可；（2）观察画出的图形，可发现S四边形AA1A2A3=S四边形AB1B2B3﹣4S△BAA3依次代入求值；（3）这个图案就是我们几何中的著名的勾股定理．

试题解析：（1）如图，正确画出图案；

（2）如图，S四边形AA1A2A3=S四边形BB1B2B3﹣4S△BAA3=（3+5）2﹣4××3×5=34

故四边形AA1A2A3的面积为34．

（3）由图可知：（a+c）2=4×ac+b2，

整理得：c2+a2=b2，

即：AB2+BC2=AC2．

这就是著名的勾股定理．