Question

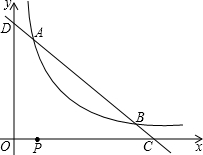
如图，在平面直角坐标系中，函数y=x与反比例函数y=

16

x

（x＞0）的图象相交于点P，以P为顶点作45°的角，角的两边分别交坐标轴于A，B，C，D．连结AB，CD．
（1）求OP的长；
（2）若点C（-6，0），求D点的坐标；
（3）△OAB的周长是否变化？若不变化，试求出△OAB的周长；若变化，请说明理由；
（4）当OP⊥AB时：①求证：OP⊥CD；②求△OAB的面积．

Answer 1

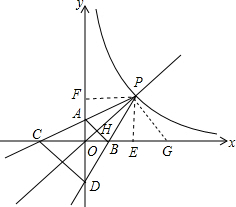
（1）作PE⊥x轴于E，PF⊥y轴于F，如图，
解方程组

y=x y= 16 x

得

x=4 y=4

或

x=-4 y=-4

（x＞0，舍去），
∴P点坐标为（4，4），
∴OP=

42+42

=4

2

；

（2）设直线PC的解析式为y=kx+b，
把C（-6，0）和P（4，4）代入得

-6k+b=0 4k+b=4

，解得

k= 2 5 b= 12 5

，
∴直线PC的解析式为y=

2

5

x+

12

5

，
∴A点坐标为（0，

12

5

），
∴AF=OF-OA=

8

5

，
把△PAF绕点P逆时针旋转90°得到△PGE，
∴∠PEG=∠PFA=90°，EG=FA，∠APG=90°，PA=PG，
而∠PEO=90°，
∴点O、E、G点共线，
∴BG=BE+EG=BE+AF，
∵∠APB=45°，
∴∠BPG=45°，
在△PBA和△PBE中

PA=PG ∠APB=∠GPB PB=PB

，
∴△PBA≌△PBE（SAS），
∴AB=BG=AF+BE，
设OB=t，则BE=4-t，AB=

8

5

+4-t=

28

5

-t，
在Rt△OAB中，∵OA²+OB²=AB²，
∴（

12

5

）²+t²=（

28

5

-t）²，解得t=

16

7

，
∴OB=

16

7

，
∵OB∥PF，
∴△DOB∽△DFP，
∴

OD

DF

=

OB

PF

，即

OD

OD+4

=

16 7

4

，解得OD=

16

3

，
∴D点坐标为（0，-

16

3

）；

（3）△OAB的周长不变化，其周长为8．
由（2）得到AB=BG=AF+BE，
∴△OAB的周长=OA+OB+AB=OA+OB+AF+BE=AF+OE=4+4=8；

（4）①证明：OP⊥AB于H，如图，
∵OP平分∠AOB，
∴OH垂直平分AB，
∴OA=OB，PA=PB，
∴OP平分∠APB，即∠APO=∠BPO，
∵∠POC=∠POA+∠AOC=135°，
∠POD=∠POB+∠BOD=135°，
∴∠POC=∠POD，
在△POC和△POB中

∠CPO=∠DPO PO=PO ∠POC=∠POD

，
∴△POC≌△POB（ASA），
∴OC=OD，
∵PO平分∠COD，
∴PO⊥CD；
②∵∠APO=∠BPO，∠APB=45°，
∴∠APO=∠BPO=22.5°，
而∠OPE=45°，
∴∠HPB=∠BPE=22.5°，
在△BHP和△BEP中

∠PHB=∠PEB ∠HPB=∠EPB PB=PB

，
∴△BHP≌△BEP（AAS），
∴PH=PE=4，
∵OP=4

2

，
∴OH=4

2

-4=4（

2

-1）
∴AB=2OH=8（

2

-1），
∴△OAB的面积=

1

2

×4（

2

-1）×8（

2

-1）=48-32

2

．