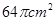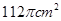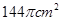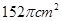题目内容
图,已知△PDC是⊙O的内接三角形,CP=CD,若将△PCD绕点P顺时针旋转,当点C刚落在⊙O上的A处时,停止旋转,此时点D落在点B处.
小题1:求证:PB与⊙O相切;
小题2:当PD=2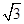 , ∠DPC=30°时,求⊙O的半径长.
, ∠DPC=30°时,求⊙O的半径长.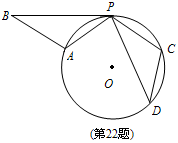
小题1:求证:PB与⊙O相切;
小题2:当PD=2
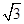 , ∠DPC=30°时,求⊙O的半径长.
, ∠DPC=30°时,求⊙O的半径长.
小题1:解:(1) 证明:连接OA、OP, 由旋转可得: △PAB≌△PCD,
∴PA="PC=DC," ∴
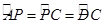 ,∠AOP="2∠D,∠APO=∠OAP="
,∠AOP="2∠D,∠APO=∠OAP=" 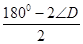
又∵∠BPA="∠DPC=∠D," ∴∠BPO=∠BPA+
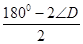 =90°
=90°∴PB与⊙O相切.
小题2:过点A作AE⊥PB,垂足为E,
∵∠BPA="30°," PB="2"
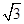 , △PAB是等腰三角形;
, △PAB是等腰三角形;∴BE="EP="
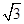 ,
,PA=
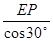 =
=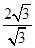 =2,
=2,又∵PB与⊙O相切于点P, ∴∠APO=60°,
∴OP=PA=2.

略

练习册系列答案
相关题目
 ⊥
⊥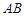 于点
于点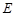 ,
, °,
°, 的半径为
的半径为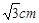 ,则弦
,则弦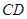 的长为
的长为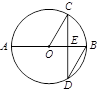 …… ( )
…… ( )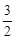 cm B.3 cm
cm B.3 cm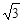 cm D.9 cm
cm D.9 cm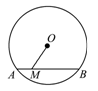


 ,
,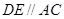 ,且
,且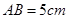 ,求DE的长.
,求DE的长.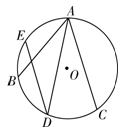
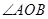 为
为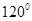 ,
, 长为
长为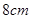 ,
,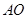 长为
长为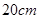 ,则图中阴影部分面积为是( )
,则图中阴影部分面积为是( )