��Ŀ����
����Ŀ����ͼ����֪������y= ![]() x2+bx+c��b��c�dz�������c��0����x��ֱ��ڵ�A��B����Aλ�ڵ�B����ࣩ����y��ĸ����ύ�ڵ�C����A������Ϊ����1��0����
x2+bx+c��b��c�dz�������c��0����x��ֱ��ڵ�A��B����Aλ�ڵ�B����ࣩ����y��ĸ����ύ�ڵ�C����A������Ϊ����1��0����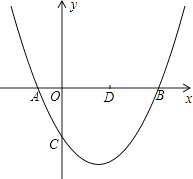
��1��b= �� ��B�ĺ�����Ϊ������������ú�c�Ĵ���ʽ��ʾ����
��2������BC������A��ֱ��AE��BC����������y= ![]() x2+bx+c���ڵ�E����D��x���ϵ�һ�㣬������Ϊ��2��0������C��D��E������ͬһֱ����ʱ���������ߵĽ���ʽ��
x2+bx+c���ڵ�E����D��x���ϵ�һ�㣬������Ϊ��2��0������C��D��E������ͬһֱ����ʱ���������ߵĽ���ʽ��
��3���ڣ�2�������£���P��x���·����������ϵ�һ�����㣬����PB��PC�������á�PBC�����ΪS��
��S��ȡֵ��Χ��
��4������PBC�����SΪ�������������ġ�PBC���и���
���𰸡�
��1��![]()
+c����2c
��2��
�⣺����һ��
��������y= ![]() x2+bx+c��y��ĸ����ύ�ڵ�C��
x2+bx+c��y��ĸ����ύ�ڵ�C��
�൱x=0ʱ��y=c������C����Ϊ��0��c����
��ֱ��BC�Ľ���ʽΪy=kx+c��
��B����2c��0����
�ੁ2kc+c=0��
��c��0��
��k= ![]() ��
��
��ֱ��BC�Ľ���ʽΪy= ![]() x+c��
x+c��
��AE��BC��
�����ֱ��AE�õ�����ʽΪy= ![]() x+m��
x+m��
�ߵ�A������Ϊ����1��0����
�� ![]() ������1��+m=0�����m=
������1��+m=0�����m= ![]() ��
��
��ֱ��AE�õ�����ʽΪy= ![]() x+
x+ ![]() ��
��
��  �����
����� ![]() ��
�� ![]() ��
��
���E������1��2c��1��c����
�ߵ�C����Ϊ��0��c������D����Ϊ��2��0����
��ֱ��CD�Ľ���ʽΪy=�� ![]() x+c��
x+c��
��C��D��E������ͬһֱ���ϣ�
��1��c=�� ![]() ����1��2c��+c��
����1��2c��+c��
��2c2+3c��2=0��
��c1= ![]() ����c��0ì�ܣ���ȥ����c2=��2��
����c��0ì�ܣ���ȥ����c2=��2��
��b= ![]() +c=��
+c=�� ![]() ��
��
�������ߵĽ���ʽΪy= ![]() x2��
x2�� ![]() x��2
x��2
��������
B����2c��0����C��0��c����
��KBC= ![]() ��
��
��AE��BC����KAE=KBC= ![]() ��
��
��A����1��0����
��lAE��y= ![]() x+
x+ ![]() ��
��
�������ߣ�y= ![]() x2+��c+
x2+��c+ ![]() ��x+c��
��x+c��
![]() x2+��c+
x2+��c+ ![]() ��x+c=
��x+c= ![]() x+
x+ ![]() ��
��
��������x2+2cx+2c��1=0��
��x+2c��1����x+1��=0��
��x1=��2c+1��x2=��1��
��E����2c+1����c+1����C��0��c����D��2��0�����㹲�ߣ�
��KCD=KDE���� ![]() ��
��
����������2c2+3c��2=0��
��ã�c=��2��c= ![]() ���ᣩ��
���ᣩ��
�������ߵĽ���ʽΪy= ![]() x2��
x2�� ![]() x��2
x��2
��3��
�⣺����һ�������P����Ϊ��x�� ![]() x2��
x2�� ![]() x��2����
x��2����
�ߵ�A������Ϊ����1��0������B����Ϊ��4��0������C����Ϊ��0����2����
��AB=5��OC=2��ֱ��BC�Ľ���ʽΪy= ![]() x��2��
x��2��
�����������
������1��x��0ʱ��0��S��S��ACB��
��S��ACB= ![]() ABOC=5��
ABOC=5��
��0��S��5��
����0��x��4ʱ������P��PG��x���ڵ�G����CB�ڵ�F��
���F������x�� ![]() x��2����
x��2����
��PF=PG��GF=���� ![]() x2��
x2�� ![]() x��2��+��
x��2��+�� ![]() x��2��=��
x��2��=�� ![]() x2+2x��
x2+2x��
��S=S��PFC+S��PFB= ![]() PFOB=
PFOB= ![]() ����
���� ![]() x2+2x����4=��x2+4x=����x��2��2+4��
x2+2x����4=��x2+4x=����x��2��2+4��
�൱x=2ʱ��S���ֵ=4��
��0��S��4��
���Ͽ�֪0��S��5
���������ٵ�P��BC�·�ʱ������P��x��Ĵ��߽�BC����F��
lBC![]() x��2����P��m��
x��2����P��m�� ![]() m2��
m2�� ![]() m��2������ôF��m��
m��2������ôF��m�� ![]() m��2����
m��2����
��FP=�� ![]() m2+2m��
m2+2m��
��S��PBC= ![]() FP��BX��CX��=2FP��
FP��BX��CX��=2FP��
S��PBC=��m2+4m=����m��2��2+4��
��˵�P��BC�·�ʱ��S��PBC�����ֵΪ4��
��P��BC�Ϸ�ʱ����S��ABC=5����S��PBC��5��
����������0��S��PBC��5��
��4��
11
������������һ��
�⣺��1����������y= ![]() x2+bx+c����A����1��0����
x2+bx+c����A����1��0����
��0= ![]() ������1��2+b������1��+c��
������1��2+b������1��+c��
��b= ![]() +c��
+c��
��������y= ![]() x2+bx+c��x��ֱ��ڵ�A����1��0����B��xB �� 0������Aλ�ڵ�B����ࣩ��
x2+bx+c��x��ֱ��ڵ�A����1��0����B��xB �� 0������Aλ�ڵ�B����ࣩ��
�ੁ1��xB��һԪ���η��� ![]() x2+bx+c=0����������
x2+bx+c=0����������
�ੁ1xB= ![]() ��
��
��xB=��2c������B�ĺ�����Ϊ��2c��
4����0��S��5��S������
��S=1��2��3��4��
�����������
������1��x��0ʱ�����PBC��BC���ϵĸ�Ϊh��
�ߵ�A������Ϊ����1��0������B����Ϊ��4��0������C����Ϊ��0����2����
��AC2=1+4=5��BC2=16+4=20��AB2=25��
��AC2+BC2=AB2 �� ��ACB=90�㣬BC���ϵĸ�AC= ![]() ��
��
��S= ![]() BCh����h=
BCh����h= ![]() =
= ![]() =
= ![]() S��
S��
���S=1����ôh= ![]() ��1=
��1= ![]() ��
�� ![]() ����ʱP����1������PBC��1����
����ʱP����1������PBC��1����
���S=2����ôh= ![]() ��2=
��2= ![]() ��
�� ![]() ����ʱP����1������PBC��1����
����ʱP����1������PBC��1����
���S=3����ôh= ![]() ��3=
��3= ![]() ��
�� ![]() ����ʱP����1������PBC��1����
����ʱP����1������PBC��1����
���S=4����ôh= ![]() ��4=
��4= ![]() ��
�� ![]() ����ʱP����1������PBC��1����
����ʱP����1������PBC��1����
������1��x��0ʱ�����������ġ�PBC����4����
����0��x��4ʱ��S=��x2+4x��
���S=1����ô��x2+4x=1����x2��4x+1=0��
�ߡ�=16��4=12��0���������������ȵ�ʵ��������ʱP����2������PBC��2����
���S=2����ô��x2+4x=2����x2��4x+2=0��
�ߡ�=16��8=8��0���������������ȵ�ʵ��������ʱP����2������PBC��2����
���S=3����ô��x2+4x=3����x2��4x+3=0��
�ߡ�=16��12=4��0���������������ȵ�ʵ��������ʱP����2������PBC��2����
���S=4����ô��x2+4x=4����x2��4x+4=0��
�ߡ�=16��16=0�������������ȵ�ʵ��������ʱP����1������PBC��1����
����0��x��4ʱ�����������ġ�PBC����7����
���Ͽ�֪�����������ġ�PBC����4+7=11����
���Դ��� ![]() +c����2c��11��
+c����2c��11��
��������
������PBC�����SΪ���������������ġ�PBC����11����
�����㾫����������Ҫ�����˸���ϵ���Ĺ�ϵ�����֪ʶ�㣬��Ҫ����һԪ���η���ax2+bx+c=0��a��0���ĸ��ɷ��̵�ϵ��a��b��c����������֮�͵��ڷ��̵�һ����ϵ�����Զ�����ϵ�����õ��̵��෴��������֮�����ڳ�������Զ�����ϵ�����õ��̲�����ȷ�����⣮

 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�


