题目内容
如图,抛物线y1=ax2-2ax+b经过A(-1,0),C(0,
)两点,与x轴交于另一点B.
(1)求此抛物线的解析式;
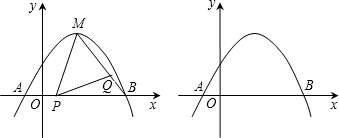
(2)若抛物线的顶点为M,点P为线段OB上一动点(不与点B重合),点Q在线段MB上移动,且∠MPQ=45°,设线段OP=x,MQ=
y2,求y2与x的函数关系式,并直接写出自变量x的取值范围;
(3)在同一平面直角坐标系中,两条直线x=m,x=n分别与抛物线交于点E、G,与(2)中的函数图象交于点F、H.问四边形EFHG能否成为平行四边形?若能,求m、n之间的数量关系;若不能,请说明理由.
| 3 |
| 2 |
(1)求此抛物线的解析式;
(2)若抛物线的顶点为M,点P为线段OB上一动点(不与点B重合),点Q在线段MB上移动,且∠MPQ=45°,设线段OP=x,MQ=
| ||
| 2 |
(3)在同一平面直角坐标系中,两条直线x=m,x=n分别与抛物线交于点E、G,与(2)中的函数图象交于点F、H.问四边形EFHG能否成为平行四边形?若能,求m、n之间的数量关系;若不能,请说明理由.

(1)∵抛物线y1=ax2-2ax+b经过A(-1,0),C(0,
)两点;
∴
,
解得
.
∴抛物线的解析式为y1=-
x2+x+
;
(2)作MN⊥AB,垂足为N.
由y1=-
x2+x+
,易得M(1,2),N(1,0),A(-1,0),B(3,0);
∴AB=4,MN=BN=2,MB=2
,∠MBN=45°;
根据勾股定理有:BM2-BN2=PM2-PN2,
∴(2
)2-22=PM2-(1-x)2…①;
又∠MPQ=45°=∠MBP,∠PMQ=∠BMP(公共角),
∴△MPQ∽△MBP,
∴PM2=MQ•MB=
y2•2
=2y2…②;
由①②得:y2=
x2-x+
;
∵0≤x<3,
∴y2与x的函数关系式为y2=
x2-x+
(0≤x<3);
(3)四边形EFHG可以为平行四边形,m、n之间的数量关系是:m+n=2(0≤m≤2且m≠1);
∵点E、G是抛物线y1=-
x2+x+
分别与直线x=m,x=n的交点,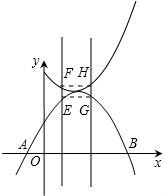
∴点E、G坐标为E(m,-
m2+m+
),G(n,-
n2+n+
);
同理,点F、H坐标为F(m,
m2-m+
),H(n,
n2-n+
).
∴EF=
m2-m+
-(-
m2+m+
)=m2-2m+1,GH=
n2-n+
-(-
n2+n+
)=n2-2n+1;
∵四边形EFHG是平行四边形,EF=GH,
∴m2-2m+1=n2-2n+1,
∴(m+n-2)(m-n)=0;
∵由题意知m≠n,
∴m+n=2(m≠1);
因此四边形EFHG可以为平行四边形,m、n之间的数量关系是m+n=2(0≤m≤2且m≠1).
| 3 |
| 2 |
∴
|
解得
|
∴抛物线的解析式为y1=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)作MN⊥AB,垂足为N.

由y1=-
| 1 |
| 2 |
| 3 |
| 2 |
∴AB=4,MN=BN=2,MB=2
| 2 |
根据勾股定理有:BM2-BN2=PM2-PN2,
∴(2
| 2 |
又∠MPQ=45°=∠MBP,∠PMQ=∠BMP(公共角),
∴△MPQ∽△MBP,
∴PM2=MQ•MB=
| ||
| 2 |
| 2 |
由①②得:y2=
| 1 |
| 2 |
| 5 |
| 2 |
∵0≤x<3,
∴y2与x的函数关系式为y2=
| 1 |
| 2 |
| 5 |
| 2 |
(3)四边形EFHG可以为平行四边形,m、n之间的数量关系是:m+n=2(0≤m≤2且m≠1);
∵点E、G是抛物线y1=-
| 1 |
| 2 |
| 3 |
| 2 |

∴点E、G坐标为E(m,-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
同理,点F、H坐标为F(m,
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴EF=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵四边形EFHG是平行四边形,EF=GH,
∴m2-2m+1=n2-2n+1,
∴(m+n-2)(m-n)=0;
∵由题意知m≠n,
∴m+n=2(m≠1);
因此四边形EFHG可以为平行四边形,m、n之间的数量关系是m+n=2(0≤m≤2且m≠1).

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目

 及其内部的抛物线部分经过平移和对称变换得到的.
及其内部的抛物线部分经过平移和对称变换得到的.

 得低于4180元,请你帮助该超市确定绿色食品销售单价x的范围(直接写出).
得低于4180元,请你帮助该超市确定绿色食品销售单价x的范围(直接写出).