题目内容
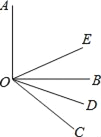
【题目】如图所示,OE,OD分别平分∠AOC和∠BOC,
(1)如果∠AOB=90°,∠BOC=38°,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β(α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律,请写出来.
【答案】(1)45° ;(2)![]() α;(3)∠DOE的大小与∠BOC的大小无关.
α;(3)∠DOE的大小与∠BOC的大小无关.
【解析】试题分析:(1)首先计算出∠AOC的度数,然后再根据角平分线的性质可得∠COE=![]() ∠AOC,∠COD=
∠AOC,∠COD=![]() ∠BOC,根据∠DOE=∠COE-∠COD代入角度计算即可;
∠BOC,根据∠DOE=∠COE-∠COD代入角度计算即可;
(2)方法与(1)相同,首先计算出∠AOC的度数,然后再根据角平分线的性质可得∠COE=![]() ∠AOC,∠COD=
∠AOC,∠COD=![]() ∠BOC,根据∠DOE=∠COE-∠COD代入角度计算即可;
∠BOC,根据∠DOE=∠COE-∠COD代入角度计算即可;
(3)根据(1)(2)的结果可得∠DOE的大小与∠BOC的大小无关.
试题解析:(1)∵∠AOB=90°,∠BOC=38°
∴∠AOC=∠AOB+∠BOC=90°+38°=128°
又∵OE,OD分别平分∠AOC和∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() ×128°=64°
×128°=64°
∠COD=![]() ∠BOC=
∠BOC=![]() ×38°=19°
×38°=19°
∴∠DOE=∠COE﹣∠COD=64°﹣19°=45°
(2)∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
又∵OE,OD分别平分∠AOC和∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() (α+β)
(α+β)
∠COD=![]() ∠BOC=
∠BOC=![]() β
β
∴∠DOE=∠COE﹣∠COD=![]() (α+β)﹣
(α+β)﹣![]() β=
β=![]() α+
α+![]() β﹣
β﹣![]() =
=![]() α;
α;

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目