Question

【题目】如图，在每个小正方形的边长为1的网格中，点A、点B均为格点．

（1）AB的长等于；
（2）若点C是以AB为底边的等腰直角三角形的顶点，点D在边AC上，且满足S△ABD= S△ABC ． 请在如图所示的网格中，用无刻度的直尺，画出线段BD，并简要说明点D的位置时如何找到的（不要求证明）． ．

Answer 1

【答案】
（1）
（2）以AB为边连接格点,构成正方形ABEF,连接对角线AE、BF,则对角线交点即为C点,正方形相邻两边分别与网格线有两个交点G、H,且为两边中点,连接GH与AE交于D点,连接BD,BD即为所求
【解析】解：（1）AB= = ；

所以答案是 （2）如图，以AB为边连接格点，构成正方形ABEF，连接对角线AE、BF，则对角线交点即为C点，正方形相邻两边分别与网格线有两个交点G、H，且为两边中点，连接GH与AE交于D点，连接BD，BD即为所求．

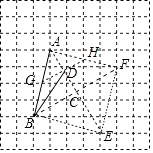
所以答案是：以AB为边连接格点，构成正方形ABEF，连接对角线AE、BF，则对角线交点即为C点，正方形相邻两边分别与网格线有两个交点G、H，且为两边中点，连接GH与AE交于D点，连接BD，BD即为所求．