题目内容
【题目】在平面直角坐标系中,O为原点,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,现将正方形OABC绕点O顺时针旋转.
(1)如图①,当点A的对应的A′落在直线y=x上时,点A′的对应坐标为;点B的对应点B′的坐标为;
(2)旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N,当A点第一次落在直线y=x上时,停止旋转.
①如图2,在正方形OABC旋转过程中,线段AM,MN,NC三者满足什么样的数量关系?请说明理由;
②当AC∥MN时,求△MBN内切圆的半径(直接写出结果即可)
【答案】
(1)A′( ![]() ,
,![]() ),B′(2
),B′(2 ![]() ,0)
,0)
(2)解:①结论:AM+CN=MN;
理由:延长BA交y轴于E点,
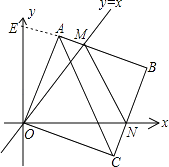
则∠AOE=45°﹣∠AOM,∠CON=90°﹣45°﹣∠AOM=45°﹣∠AOM,
∴∠AOE=∠CON,
又∵OA=OC,∠OAE=180°﹣90°=90°=∠OCN,
在△OAE和△OCN中,
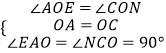 ,
,
∴△OAE≌△OCN(ASA),
∴OE=ON,AE=CN,
在△OME和△OMN中
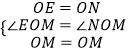 ,
,
∴△OME≌△OMN(SAS).
∴MN=ME=AM+AE.
∴MN=AM+CN,
②∵MN∥AC,
∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°,
∴∠BMN=∠BNM,
∴BM=BN,∵BA=BC,
∴AM=NC,
设AM=NC=a,则MN=2a,
在Rt△BMN中,(2a)2=(2﹣a)2+(2﹣a)2,
解得a=2 ![]() ﹣2或﹣2
﹣2或﹣2 ![]() ﹣2(舍弃),
﹣2(舍弃),
∴MN=4 ![]() ﹣4,BM=BN=4﹣2
﹣4,BM=BN=4﹣2 ![]() ,
,
∴△BMN的内切圆半径r= ![]() =
= ![]() =6﹣4
=6﹣4 ![]()
【解析】解:(1)如图1中,作A′H⊥OB′于H.
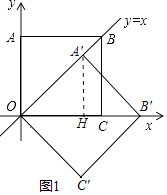
∵四边形ABCD是正方形,
∴OA=OC=BC=AB=2,∠BOC=45°=45,OB=2 ![]() ,
,
∵OA′=2,
∴AH=OH= ![]() ,
,
∴A′( ![]() ,
, ![]() ),
),
∵旋转角为45°,
∴B′在x轴上,
∴B′(2 ![]() ,0),
,0),
所以答案是A′( ![]() ,
, ![]() ),B′(2
),B′(2 ![]() ,0);
,0);

 新思维寒假作业系列答案
新思维寒假作业系列答案【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人 | 笔试成绩/分 | 面试成绩/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.