题目内容
【题目】如图,在△ABC中,已知AB=AC,D、E、B、C在同一条直线上,且AB2=BDCE,求证:△ABD∽△ECA.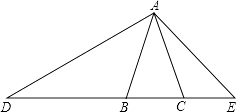
【答案】证明:
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
∵AB2=BDCE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴△ABD∽△ECA
【解析】由条件可得到∠ABD=∠ACE,结合AB2=BDCE和AB=AC,可得到 ![]() =
= ![]() ,即可证得结论.
,即可证得结论.
【考点精析】掌握相似三角形的判定是解答本题的根本,需要知道相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).

练习册系列答案
相关题目
【题目】某超市的某种商品一周内每天的进价与售价信息和实际每天的销售量情况如图表所示:
进价与售价折线图(单位:元/斤)

实际销售量表(单位:斤)
日期 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
销售量 | 30 | 40 | 35 | 30 | 50 | 60 | 50 |
则下列推断不合理的是( )
A. 该商品周一的利润最小
B. 该商品周日的利润最大
C. 由一周中的该商品每天售价组成的这组数据的众数是4(元/斤)
D. 由一周中的该商品每天进价组成的这组数据的中位数是3(元/斤)



