题目内容
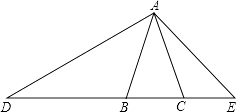
【题目】如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点. 
【答案】解:在等腰△ABC中,顶角∠A=36°,
所以∠ABC=∠C=72°,
∵BD为∠ABC的平分线,
∴∠ABD=∠DBC=36°,
在△ACB和△BCD中,∠BDC=72°
∵∠C=∠C,∠A=∠CBD=36°,
∴△ACB∽△BCD,
∴AC:BC=BC:DC;
∵∠A=∠ABD,
∴AD=BD,
∵∠DBC=36°,∠C=72°,
∴∠BDC=72°,
∴BD=BC,
∴AD=BC,
∴AC:AD=AD:DC;
即点D是AC的黄金分割点
【解析】欲证点D是AC的黄金分割点,就是证明AC:AD=AD:DC,根据角平分线的性质以及已知条件推知∠C=∠C,∠A=∠CBD=36°,所以△ACB∽△BCD;然后根据相似三角形的对应边成比例求得AC:AD=AD:DC;最后由等腰三角形的性质得到:BC=BD=DA,代换即可.
【考点精析】通过灵活运用黄金分割,掌握把线段AB分成两条线段AC,BC(AC>BC),并且使AC是AB和BC的比例中项,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=0.618AB即可以解答此题.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.

【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 | 身高 |
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?