ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋŌŅÖŠÅŨÎïÏßy=ax2+bx+cÓëxÖá―ŧÓÚAĢĻ1ĢŽ0ĢĐĢŽBĢĻ3ĢŽ0ĢĐĢŽÓëyÖá―ŧÓÚCĢĻ0ĢŽĐ2ĢĐĢŽķĨĩãΊDĢŽĩãEĩÄŨøąęΊĢĻ0ĢŽĐ1ĢĐĢŽļÃÅŨÎïÏßÓÚBE―ŧÓÚÁíŌŧĩãFĢŽÁŽ―ÓBC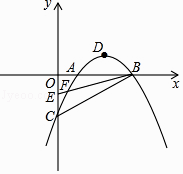
ĢĻ1ĢĐĮóļÃÅŨÎïÏßĩÄ―âÎöĘ―Ģŧ
ĢĻ2ĢĐČôĩãHĢĻ1ĢŽyĢĐÔÚBCÉÏĢŽÁŽ―ÓFHĢŽĮóĄũFHBĩÄÃæŧýĢŧ
ĢĻ3ĢĐŌŧķŊĩãMīÓĩãDģö·ĒĢŽŌÔÃŋÃë1ļöĩĨÎŧĩÄËŲķČŅØÆ―ÐÐÓÚyÖá·―ÏōÏōÉÏÔËķŊĢŽÁŽ―ÓOMĢŽBMĢŽÉčÔËķŊĘąžäΊtÃëĢĻtĢū0ĢĐĢŽĩãMÔÚÔËķŊđýģĖÖÐĢŽĩątΊšÎÖĩĘąĢŽĄÏOMB=90ĄãĢŋ
ĢĻ4ĢĐÔÚxÖáÉÏ·―ĩÄÅŨÎïÏßÉÏĢŽĘĮ·ņīæÔÚĩãPĢŽĘđĩÃĄÏPBFąŧBAÆ―·ÖĢŋČôīæÔÚĢŽÖą―ÓÐīģöĩãPĩÄŨøąęĢŧČôēŧīæÔÚĢŽĮëËĩÃũĀûÓÉĢŪ
Ąūīð°ļĄŋ
ĢĻ1ĢĐ
―âĢšÉčÅŨÎïÏß―âÎöĘ―ÎŠy=aĢĻxĐ1ĢĐĢĻxĐ3ĢĐĢŽ
°ŅCĢĻ0ĢŽĐ2ĢĐīúČëĩÃaĢĻĐ1ĢĐĢĻĐ3ĢĐ=Đ2ĢŽ―âĩÃa=Đ ![]() ĢŽ
ĢŽ
ËųŌÔÅŨÎïÏß―âÎöĘ―ÎŠy=Đ ![]() ĢĻxĐ1ĢĐĢĻxĐ3ĢĐĢŽžīy=Đ
ĢĻxĐ1ĢĐĢĻxĐ3ĢĐĢŽžīy=Đ ![]() x2+
x2+ ![]() xĐ2
xĐ2
ĢĻ2ĢĐ
―âĢšÉčÖąÏßBEĩÄ―âÎöĘ―ÎŠy=mx+nĢŽ
°ŅBĢĻ3ĢŽ0ĢĐĢŽEĢĻ0ĢŽĐ1ĢĐīúČëĩÃ ![]() ĢŽ―âĩÃ
ĢŽ―âĩÃ 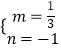 ĢŽ
ĢŽ
ĄāÖąÏßBEĩÄ―âÎöĘ―ÎŠy= ![]() xĐ1ĢŽ
xĐ1ĢŽ
ÍŽŅų·―·ĻŋÉĮóĩÃÖąÏßBCĩÄ―âÎöĘ―ÎŠy= ![]() xĐ2ĢŽ
xĐ2ĢŽ
―â·―ģĖŨé 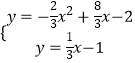 ĩÃ
ĩÃ ![]() ŧō
ŧō 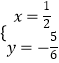 ĢŽÔōFĢĻ
ĢŽÔōFĢĻ ![]() ĢŽĐ
ĢŽĐ ![]() ĢĐĢŧ
ĢĐĢŧ
ĩąx=1ĘąĢŽy= ![]() Đ2=Đ
Đ2=Đ ![]() ĢŽÔōHĢĻ1ĢŽĐ
ĢŽÔōHĢĻ1ĢŽĐ ![]() ĢĐĢŽ
ĢĐĢŽ
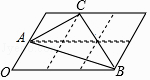
ÁŽ―ÓAH―ŧBEÓÚQĢŽČįÍž1ĢŽĄßAĢĻ1ĢŽ0ĢĐĢŽHĢĻ1ĢŽĐ ![]() ĢĐĢŽ
ĢĐĢŽ
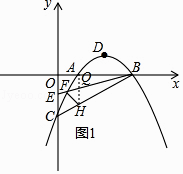
ĄāAHĄÍxÖáĢŽ
ĄāQĢĻ1ĢŽĐ ![]() ĢĐĢŽ
ĢĐĢŽ
ĄāHQ=Đ ![]() +
+ ![]() =
= ![]() ĢŽ
ĢŽ
ĄāSĄũFHB=SĄũBHQ+SĄũFHQ= ![]() ĄÁ
ĄÁ ![]() ĄÁĢĻ3Đ
ĄÁĢĻ3Đ ![]() ĢĐ
ĢĐ ![]()
ĢĻ3ĢĐ
―âĢšĩąx=2ĘąĢŽy=Đ ![]() x2+
x2+ ![]() xĐ2=
xĐ2= ![]() ĢŽÔōDĢĻ2ĢŽ
ĢŽÔōDĢĻ2ĢŽ ![]() ĢĐĢŽ
ĢĐĢŽ
ĄāÅŨÎïÏßĩÄķÔģÆÖáΊֹÏßx=2ĢŽ
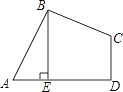
ÖąÏßx=2―ŧxÖáÓÚNĢŽČįÍž2ĢŽMN=t+ ![]() ĢŽON=2ĢŽBN=1ĢŽ
ĢŽON=2ĢŽBN=1ĢŽ
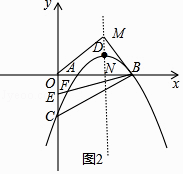
ĄßĄÏOMB=90ĄãĢŽžīĄÏOMN+ĄÏBMN=90ĄãĢŽ
ķøĄÏOMN+ĄÏMON=90ĄãĢŽ
ĄāĄÏMON=ĄÏBMNĢŽ
ĄāRtĄũOMNĄŨRtĄũMBNĢŽ
ĄāMNĢšBN=ONĢšMNĢŽžīMN2=BNONĢŽ
ĄāĢĻt+ ![]() ĢĐ2=1ĄÁ2ĢŽ―âĩÃt1=
ĢĐ2=1ĄÁ2ĢŽ―âĩÃt1= ![]() Đ
Đ ![]() ĢŽt2=Đ
ĢŽt2=Đ ![]() Đ
Đ ![]() ĢĻÉáČĨĢĐĢŽ
ĢĻÉáČĨĢĐĢŽ
ĄāĩątΊ ![]() Đ
Đ ![]() ĘąĢŽĄÏOMB=90ĄãĢŧ
ĘąĢŽĄÏOMB=90ĄãĢŧ
ĢĻ4ĢĐ
―âĢšīæÔÚĢŪ
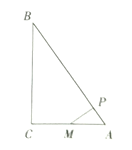
ČįÍž3ĢŽBP―ŧyÖáÓÚGĢŽ
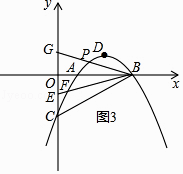
ĄßABÆ―·ÖĄÏFBPĢŽ
ĄāĄÏGBO=ĄÏEOBĢŽ
ĄāĩãGÓëĩãEđØÓÚxÖáķÔģÆĢŽ
ĄāGĢĻ0ĢŽ1ĢĐĢŽ
ÉčÖąÏßBGĩÄ―âÎöĘ―ÎŠy=px+qĢŽ
°ŅGĢĻ0ĢŽ1ĢĐĢŽBĢĻ3ĢŽ0ĢĐīúČëĩÃ ![]() ĢŽ―âĩÃ
ĢŽ―âĩÃ 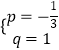 ĢŽ
ĢŽ
ĄāÖąÏßBQĩÄ―âÎöĘ―ÎŠy=Đ ![]() x+1ĢŽ
x+1ĢŽ
―â·―ģĖŨé 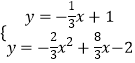 ĩÃ
ĩÃ ![]() ŧō
ŧō ![]() ĢŽ
ĢŽ
ĄāPĩãŨøąęΊĢĻ ![]() ĢŽ
ĢŽ ![]() ĢĐĢŪ
ĢĐĢŪ
Ąū―âÎöĄŋĢĻ1ĢĐÉč―ŧĩãĘ―ÅŨÎïÏß―âÎöĘ―ÎŠy=aĢĻxĐ1ĢĐĢĻxĐ3ĢĐĢŽČŧšó°ŅCĩãŨøąęīúČëĮóģöažīŋÉĩÃĩ―ÅŨÎïÏß―âÎöĘ―ĢŧĢĻ2ĢĐÏČĀûÓÃīýķĻÏĩĘý·ĻĮóģöÖąÏßBEĩÄ―âÎöĘ―ÎŠy= ![]() xĐ1ĢŽÖąÏßBCĩÄ―âÎöĘ―ÎŠy=
xĐ1ĢŽÖąÏßBCĩÄ―âÎöĘ―ÎŠy= ![]() xĐ2ĢŽÔŲ―â·―ģĖŨé
xĐ2ĢŽÔŲ―â·―ģĖŨé 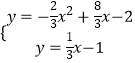 ĩÃFĢĻ
ĩÃFĢĻ ![]() ĢŽĐ
ĢŽĐ ![]() ĢĐĢŧ―ÓŨÅČ·ķĻHĢĻ1ĢŽĐ
ĢĐĢŧ―ÓŨÅČ·ķĻHĢĻ1ĢŽĐ ![]() ĢĐĢŽÁŽ―ÓAH―ŧBEÓÚQĢŽČįÍž1ĢŽĀûÓÃĩãAšÍHĩÄšáŨøąęĖØÕũĩÃĩ―AHĄÍxÖáĢŽËųŌÔQĢĻ1ĢŽĐ
ĢĐĢŽÁŽ―ÓAH―ŧBEÓÚQĢŽČįÍž1ĢŽĀûÓÃĩãAšÍHĩÄšáŨøąęĖØÕũĩÃĩ―AHĄÍxÖáĢŽËųŌÔQĢĻ1ĢŽĐ ![]() ĢĐĢŽČŧšóĀûÓÃČý―ĮÐÎÃæŧýđŦĘ―ĢŽĀûÓÃSĄũFHB=SĄũBHQ+SĄũFHQ―øÐОÆËãĢŧĢĻ3ĢĐÏČĮóģöDĢĻ2ĢŽ
ĢĐĢŽČŧšóĀûÓÃČý―ĮÐÎÃæŧýđŦĘ―ĢŽĀûÓÃSĄũFHB=SĄũBHQ+SĄũFHQ―øÐОÆËãĢŧĢĻ3ĢĐÏČĮóģöDĢĻ2ĢŽ ![]() ĢĐĢŽÖąÏßx=2―ŧxÖáÓÚNĢŽČįÍž2ĢŽÖĪÃũRtĄũOMNĄŨRtĄũMBNĩÃĩ―MN2=BNONĢŽžīĢĻt+
ĢĐĢŽÖąÏßx=2―ŧxÖáÓÚNĢŽČįÍž2ĢŽÖĪÃũRtĄũOMNĄŨRtĄũMBNĩÃĩ―MN2=BNONĢŽžīĢĻt+ ![]() ĢĐ2=1ĄÁ2ĢŽČŧšó―â·―ģĖžīŋÉĢŧĢĻ4ĢĐČįÍž3ĢŽBP―ŧyÖáÓÚGĢŽĀûÓÃABÆ―·ÖĄÏFBPĩÃĩ―ĩãGÓëĩãEđØÓÚxÖáķÔģÆĢŽÔōGĢĻ0ĢŽ1ĢĐĢŽÔŲĀûÓÃīýķĻÏĩĘý·ĻĮóģöÖąÏßBQĩÄ―âÎöĘ―ÎŠy=Đ
ĢĐ2=1ĄÁ2ĢŽČŧšó―â·―ģĖžīŋÉĢŧĢĻ4ĢĐČįÍž3ĢŽBP―ŧyÖáÓÚGĢŽĀûÓÃABÆ―·ÖĄÏFBPĩÃĩ―ĩãGÓëĩãEđØÓÚxÖáķÔģÆĢŽÔōGĢĻ0ĢŽ1ĢĐĢŽÔŲĀûÓÃīýķĻÏĩĘý·ĻĮóģöÖąÏßBQĩÄ―âÎöĘ―ÎŠy=Đ ![]() x+1ĢŽČŧšó―â·―ģĖŨé
x+1ĢŽČŧšó―â·―ģĖŨé 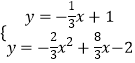 žīŋÉĩÃĩ―PĩãŨøąęĢŪ
žīŋÉĩÃĩ―PĩãŨøąęĢŪ

ĄūĖâÄŋĄŋΊÁËīŦģÐÓÅÐãīŦÍģÎÄŧŊĢŽÎŌĘÐŨéÖŊÁËŌŧīÎģõČýÄęžķ1 200ÃûŅ§ÉúēΞÓĩÄĄ°ššŨÖĖýÐīĄąīóČüĢŽÎŠÁËļüšÃĩØÁË―âąūīÎīóČüĩÄģÉžĻ·ÖēžĮéŋöĢŽËæŧúģéČĄÁË100ÃûŅ§ÉúĩÄģÉžĻ(Âú·Ö50·Ö)ĢŽÕûĀíĩÃĩ―ČįÏÂĩÄÍģžÆÍžąíĢš
ģÉžĻ(·Ö) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
ČËĘý | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
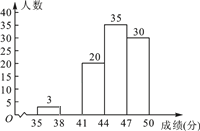
ģÉžĻ·ÖŨé | ÆĩĘý | ÆĩÂĘ(°Ų·ÖąČ) |
35ĄÜx<38 | 3 | 0.03 |
38ĄÜx<41 | a | 0.12 |
41ĄÜx<44 | 20 | 0.20 |
44ĄÜx<47 | 35 | 0.35 |
47ĄÜxĄÜ50 | 30 | b |
ĮëļųūÝËųĖáđĐĩÄÐÅÏĒ―âīðÏÂÁÐÎĘĖâĢš
(1)ÆĩÂĘÍģžÆąíÖÐaĢ―________ĢŽbĢ―_______Ģŧ
(2)ĮëēđČŦÆĩĘý·ÖēžÖą·―ÍžĢŧ
(3)ĮëļųūÝģéŅųÍģžÆ―áđûĢŽđĀžÆļÃīÎīóČüÖÐģÉžĻēŧĩÍÓÚ41·ÖĩÄŅ§ÉúÓÐķāÉŲČËĢŋ