题目内容
观察下列运算并填空:
1×2×3×4+1=25=52;
2×3×4×5+1=121=112:
3×4×5×6+1=361=192;…
根据以上结果,猜想并研究:(n+1)(n+2)(n+3)(n+4)+1=______.
1×2×3×4+1=25=52;
2×3×4×5+1=121=112:
3×4×5×6+1=361=192;…
根据以上结果,猜想并研究:(n+1)(n+2)(n+3)(n+4)+1=______.
由1×2×3×4+1=25=52=(02+5×0+5)2;
2×3×4×5+1=121=112=(12+5×1+5)2;
3×4×5×6+1=361=192=(22+5×2+5)2,…
观察发现:(n+1)(n+2)(n+3)(n+4)+1=(n2+5n+5)2.
证明:等式左边=(n+1)(n+2)(n+3)(n+4)+1
=(n2+3n+2)(n2+7n+12)+1
=n4+7n3+12n2+3n3+21n2+36n+2n2+14n+25
=n4+10n3+35n2+50n+25
=n4+2n2(5n+5)+(5n+5)2
=(n2+5n+5)2=等式右边.
故答案为:(n2+5n+5)2
2×3×4×5+1=121=112=(12+5×1+5)2;
3×4×5×6+1=361=192=(22+5×2+5)2,…
观察发现:(n+1)(n+2)(n+3)(n+4)+1=(n2+5n+5)2.
证明:等式左边=(n+1)(n+2)(n+3)(n+4)+1
=(n2+3n+2)(n2+7n+12)+1
=n4+7n3+12n2+3n3+21n2+36n+2n2+14n+25
=n4+10n3+35n2+50n+25
=n4+2n2(5n+5)+(5n+5)2
=(n2+5n+5)2=等式右边.
故答案为:(n2+5n+5)2

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

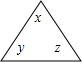 表示3xyz,“方框”
表示3xyz,“方框” 表示-abdc,求
表示-abdc,求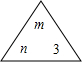 ×
× =______.
=______.