题目内容
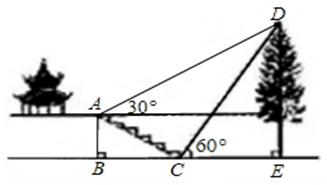
如图,我校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1: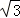 ,且B、C、E三点在同一条直线上.
,且B、C、E三点在同一条直线上.
请根据以上条件求出树DE的高度.
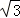 ,且B、C、E三点在同一条直线上.
,且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度.

9米.
试题分析:过点A作AF⊥DE于F,可得四边形ABEF为矩形,设DE=x,在Rt△DCE和Rt△ABC中分别表示出CE,BC的长度,求出DF的长度,然后在Rt△ADF中表示出AF的长度,根据AF=BE,代入解方程求出x的值即可.
如图,过点A作AF⊥DE于F,
则四边形ABEF为矩形,
∴AF=BE,EF=AB=3,
设DE=x,
在Rt△CDE中,CE=
 ,
,在Rt△ABC中,
∵
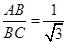 ,AB=3,
,AB=3,∴BC=3
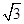 ,
,在Rt△AFD中,DF=DE-EF=x-3,
∴AF=
 ,
,∵AF=BE=BC+CE,
∴
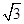 (x-3)=3
(x-3)=3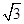 +
+ x,
x,解得x=9.
答:树高为9米.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 .
.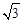 +2cos30°的值为 .
+2cos30°的值为 .
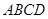 和一个长为2、宽为1的长方形
和一个长为2、宽为1的长方形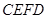 拼在一起,构成一个大的长方形
拼在一起,构成一个大的长方形 .现将小长方形
.现将小长方形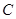 顺时针旋转至
顺时针旋转至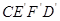 ,旋转角为
,旋转角为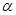 .
.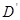 恰好落在
恰好落在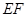 边上时,求旋转角
边上时,求旋转角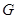 为
为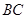 的中点,且0°<
的中点,且0°<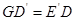 ;
;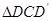 与
与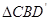 全等(0°<
全等(0°< 沿CD边竖直向上平移t个单位,设移动后小长方形边直线
沿CD边竖直向上平移t个单位,设移动后小长方形边直线 与BC交于点H,若DH∥FC,求上述运动变换过程中
与BC交于点H,若DH∥FC,求上述运动变换过程中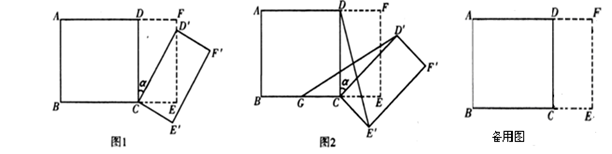


 .
.