题目内容
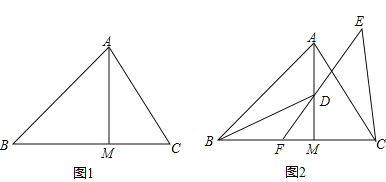
【题目】在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.
(1)如图1,若AB=3![]() ,BC=5,求AC的长;
,BC=5,求AC的长;
(2)如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)先由AM=BM=ABcos45°=3可得CM=2,再由勾股定理可求出AC的长;
(2)延长EF到点G,使得FG=EF,证ΔBMD≌ΔANC得AC=BD,再证ΔBFG≌ΔCFE得BG=CE,∠G=∠E,从而得BD=BG=CE,即可得∠BDG=∠G=∠E.
试题解析:(1)∵∠ABM=45°,AM⊥BM,
∴AM=BM=ABcos45°=3![]() ×
×![]() =3,
=3,
则CM=BC﹣BM=5﹣2=2,
∴AC=![]() ;
;
(2)延长EF到点G,使得FG=EF,连接BG.
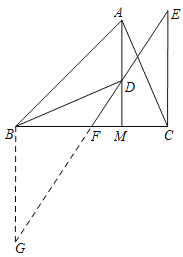
由DM=MC,∠BMD=∠AMC,BM=AM,
∴△BMD≌△AMC(SAS),
∴AC=BD,
又CE=AC,
因此BD=CE,
由BF=FC,∠BFG=∠EFC,FG=FE,
∴△BFG≌△CFE,
故BG=CE,∠G=∠E,
所以BD=BG=CE,
因此∠BDG=∠G=∠E.
考点:1.全等三角形的判定与性质;2.勾股定理.

【题目】五一节期间,电器市场火爆,某商店需要购进一批电视机和洗衣机,根据市场调查,电视机与洗衣机的进价和售价如下表:
类别 | 电视机 | 洗衣机 |
进价(元/台) | 1800 | 1500 |
售价(元/台) | 2000 | 1600 |
若该商店计划电视机和洗衣机共100台,设购进电视机x台,获得的总利润y元.
(1)求出y与x的函数关系;
(2)已知商店最多筹集资金161800元,求购进多少台电视机,才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最多利润.(利润=售价﹣进价)