题目内容
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则B6B7的边长为( )

A. 6![]() B. 12
B. 12![]() C. 32
C. 32![]() D. 64
D. 64![]()
【答案】C
【解析】
根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2…进而得到A7B7=26B1A2=26=64,B6A7=![]() A7B7=32,再根据勾股定理即可解答.
A7B7=32,再根据勾股定理即可解答.
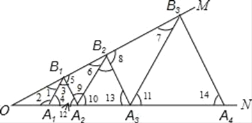
解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2=2,B3A3=2B2A3,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
以此类推:A7B7=26B1A2=26=64,B6A7=![]() A7B7=32,△B7B6A7是直角三角形,∠B7B6A7=90°,
A7B7=32,△B7B6A7是直角三角形,∠B7B6A7=90°,
∴B6B7=![]() =
=![]() =32
=32![]() .
.
故选:C.

【题目】先填写表,通过观察后再回答问题:
a | 0 | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| 0 | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ,y= ;
(2)从表格中探究a与![]() 数位变化可以发现:当被开方数a每扩大100倍时,
数位变化可以发现:当被开方数a每扩大100倍时,![]() 扩大_________倍,请你利用这个规律解决下面两个问题:
扩大_________倍,请你利用这个规律解决下面两个问题:
①已知![]() ,则
,则![]() ;
;
②已![]() ,若
,若![]() ,用含m的代数式表示n,则n= ;
,用含m的代数式表示n,则n= ;
(3)请根据表格提示,试比较![]() 与a的大小.
与a的大小.