题目内容
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上, ΔAEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中结论正确的个数为( )
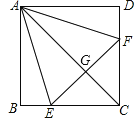
A. 2个 B. 3个 C. 4个 D. 5个
【答案】B
【解析】分析:本题是四边形的综合题,利用三角形的知识解决即可.
解析:∵四边形ABCD是正方形,∴AB=AD,∵△AEF是等边三角形,∴AE=AF,在Rt△ABE和Rt△ADF中,![]() ,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∴①说法正确;∵BC=DC,∴BC-BE=CD-DF,∴CE=CF,∴△ECF是等腰直角三角形,∴∠CFE=45°∴∠AFD=75°∴∠DAF=15°∴②正确;∵AC是正方形ABCD的对角线,∴∠BCA=45°∴AC⊥EF又CE=CF∴AC垂直平分EF,∴③正确;在AD上取一点G,连接FG,使AG=GF,则∠DAF=∠GFA=15°,∴∠DGF=2∠DAF=30°,
,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∴①说法正确;∵BC=DC,∴BC-BE=CD-DF,∴CE=CF,∴△ECF是等腰直角三角形,∴∠CFE=45°∴∠AFD=75°∴∠DAF=15°∴②正确;∵AC是正方形ABCD的对角线,∴∠BCA=45°∴AC⊥EF又CE=CF∴AC垂直平分EF,∴③正确;在AD上取一点G,连接FG,使AG=GF,则∠DAF=∠GFA=15°,∴∠DGF=2∠DAF=30°,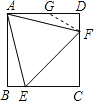
设DF=1,则AG=GF=2,DG=![]() ,∴AD=CD=2+
,∴AD=CD=2+![]() ,CF=CE=CD-DF=1+
,CF=CE=CD-DF=1+![]() ,∴EF=
,∴EF=![]() CF=
CF=![]() +
+![]() ,而BE+DF=2,∴④说法错误;
,而BE+DF=2,∴④说法错误;
∵S△ABE+SADF=2S△ABE=2×![]() AD×DF=2+
AD×DF=2+![]() ,
,
S△CEF=![]() CE×CF=
CE×CF=![]() ,∴⑤正确
,∴⑤正确
故选B.
定睛:本题考察的知识点为正方形的性质、全等三角形的判定与性质、等边三角形的性质.利用知识点逐个进行证明.

练习册系列答案
相关题目