题目内容
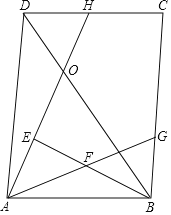
【题目】如图,已知正方形ABCD,对角线AC、BD交于点O,点E在对角线BD上,连接AE.点G是AD延长线上一点,DF平分∠GDC,且DF=BE,连接FB、FC,FB与AC交于点M.
(1)若点E是BD的三等分点(DE<BE),BF=![]() ,求△ABE的面积;
,求△ABE的面积;
(2)求证:DE=2CM.
【答案】(1)18;(2)证明见解析.
【解析】
(1)由点E是BD的三等分点,设BE=DF=2x,DE=x. 在Rt△BDF中,根据勾股定理得BD+DF=BF,即可求出![]() 的值,根据三角形的面积公式求解即可.
的值,根据三角形的面积公式求解即可.
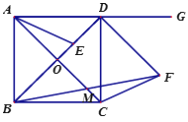
(2)延长DF、BC交于点H.证明△EBA≌△FDC,根据全等三角形的性质得到AE=CF,∠AEB=∠CFD,再证明△AED≌△CFH,即可证明.
解:(1)由题意易得∠BDF=90°,
∵点E是BD的三等分点(DE<BE)
∴设BE=DF=2x,DE=x.
在Rt△BDF中,∠BDF=90°
∵BD+DF=BF
∴9x+4x=156解得x=![]()
∴BE=2x=![]() ,AO=
,AO=![]() BD=
BD=![]()
∴△ABE面积=![]() ·BE·AO=
·BE·AO=![]() =18.
=18.
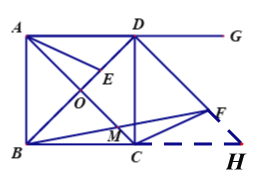
(2)同时延长DF、BC交于点H.
∵O是BD中点,OC∥DF
∴M是BF中点,C是BH中点.
∴CM是△BFH的中位线.
即FH=2CM.
在△EBA与△FDC中
EB=FD;∠ABE=∠FDC=45°,CD=AB
∴△EBA≌△FDC(SAS).
∴AE=CF,∠AEB=∠CFD
∴∠AED=∠CFH.
∵CM∥FH
∴∠H=∠ACB=∠ADB=45°.
在△AED与△CFH中
∠ADB=∠H,∠AED=∠CFH,AE=CF
∴△AED≌△CFH(AAS)
∴DE=FH=2CM.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目