题目内容
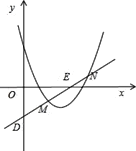
【题目】如图，已知抛物线
，过点D（0，
）的直线与抛物线交于点M、N，与
轴交于点E，且点M、N关于点E对称，求直线MN的解析式．
【答案】y=x
.
【解析】
设直线MN的解析式为y=kx（k≠0）．根据一元二次方程x2-4x+3=0的根求得点E的坐标．把点E的坐标代入求得k的值即可．
过点D(0，)的直线与抛物线交于M(xM,yM)、N(xN,yN)两点，与x轴交于点E，使得M、N两点关于点E对称。
设直线MN的解析式为：y=kx，
则有：YM+YN=0,
由
，
x24x+3=kx，
移项后合并同类项得x2(k+4)x+
=0，
∴xM+xN=4+k.
∴yM+yN=kxM+kxN=k(xM+xN)5=0，
∴yM+yN=k(xM+xN)=5，
即k(k+4)5=0，
∴k=1或k=5.
当k=5时,方程x2(k+4)x+=0的判别式△<0，直线MN与抛物线无交点，
∴k=1，
∴直线MN的解析式为y=x.
练习册系列答案
ABC考王全优卷系列答案
相关题目
