题目内容
【题目】已知:四边形ABCD中,∠ABC=∠ADC=90°,AB=BC,连接BD.
(1)画出示意图;
(2)请问:DB平分∠ADC吗?请给出结论,并说明理由.
【答案】(1)见解析;(2)DB平分∠ADC,理由见解析.
【解析】
(1)根据题意画出图形即可;
(2)作BM⊥AD于M,BN⊥DC交DC的延长线于N,根据AAS证明△ABM≌△CBN,得出BM=BN,再根据HL证明△DBM≌△DBN即可解决问题.
解:(1)根据题意画出图形如下:
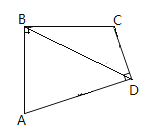
(2)DB平分∠ADC,理由:
作BM⊥AD于M,BN⊥DC交DC的延长线于N,
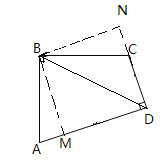
∵∠ABC=∠ADC=90°,
∴∠MBN=90°,
∴∠ABM=∠CBN,
∵BM⊥AD于M,BN⊥DC交DC的延长线于N,
∴∠AMB=∠CNB=90°,
又∵AB=BC,
∴△ABM≌△CBN,
∴BM=BN,
∵BD=BD,
∴Rt△DBM≌Rt△DBN,
∴∠BDM=∠BDN,即DB平分∠ADC.

练习册系列答案
相关题目