Question

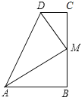
【题目】如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC，∠CMD=35°，∠MAB的度数是________．

Answer 1

【答案】35°．

【解析】

过点M作MN⊥AD于N，根据角平分线的性质可得MC=MN，可求出MB=MN，再根据到角的两边距离相等的点在角的平分线上判断出AM是∠BAD的平分线，然后求出∠AMB，再根据直角三角形两锐角互余求解即可．

解：如图，过点M作MN⊥AD于N，

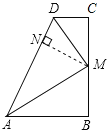
∵∠C=90°，DM平分∠ADC，
∴MC=MN，
∴∠CMD=∠NMD =35°，
∵M是BC的中点，
∴MB=MC，
∴MB=MN，
∵∠B=90°，
∴AM是∠BAD的平分线，∠AMB=∠AMN，
∵∠CMD=∠NMD =35°，
∴∠AMB=（180°-35°×2）=55°，
∴∠MAB=90°-∠AMB=90°-55°=35°．
故答案为：35°．