题目内容
【题目】如图1,一张三角形ABC纸片,点D、E分别是△ABC边上两点. 研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是 . 
【答案】∠BDA′=2∠A;∠BDA′+∠CEA′=2∠A;∠BDA′﹣∠CEA′=2∠A
【解析】解:1)∠BDA′与∠A的数量关系是∠BDA′=2∠A; 2)∠BDA′+∠CEA′=2∠A,
理由:在四边形ADA′E中,∠A+∠DA′E+∠ADA′+∠A′EA=360°,
∴∠A+∠DA′E=360°﹣∠ADA′﹣∠A′EA,
∵∠BDA′+∠ADA′=180°,∠CEA′+∠A′EA=180°,
∴∠BDA′+∠CEA′=360°﹣∠ADA′﹣∠A′EA,
∴∠BDA′+∠CEA′=∠A+∠DA′E,
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠DA′E,
∴∠BDA′+∠CEA′=2∠A;
3)∠BDA′﹣∠CEA′=2∠A.
理由:DA′交AC于点F,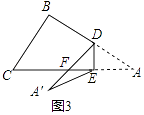
∵∠BDA′=∠A+∠DFA,∠DFA=∠A′+∠CEA′,
∴∠BDA′=∠A+∠A′+∠CEA′,
∴∠BDA′﹣∠CEA′=∠A+∠A′,
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠DA′E,
∴∠BDA′﹣∠CEA′=2∠A.
所以答案是:∠BDA′=2∠A;∠BDA′+∠CEA′=2∠A;∠BDA′﹣∠CEA′=2∠A.
【考点精析】掌握三角形的内角和外角是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案



