题目内容
【题目】如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图像与y轴相交于点B(0,—5),与x轴交于点C.
(1)判断△AOB的形状并说明理由;
(2)请写出当y1>y2时x的取值范围;
(3)若将直线AB绕点A旋转,使△AOC的面积为8,求旋转后直线AB的函数解析式;
(4)在x轴上求一点P使△POA为等腰三角形,请直接写出所有符合条件的点P的坐标.
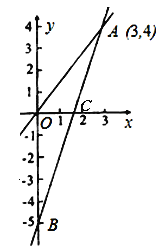
【答案】(1)△AOB是等腰三角形,证明详见解析;(2)x<3;(3)y=-4x+16或y=![]() ;(4) P(5,0)或(-5,0)或(6,0)或(
;(4) P(5,0)或(-5,0)或(6,0)或(![]() ).
).
【解析】
(1)根据A的坐标求得OA和OB的长度即可判断;
(2)根据图象当y1>y2时即y1的函数值大,即对相同的x的值,y1对应的图象的点在上边,根据图象即可写出;
(3)首先根据三角形的面积公式求得OC的长,即可得到C的坐标,利用待定系数法即可求解;
(4)已知等腰三角形POA中的一边OA,分1)OA是底边;2)OA是腰,且A是顶角的顶点;3)OA是腰,且O是顶角的顶点.三种情况进行讨论.
解:(1)OA=![]() =5,则OA=OB,
=5,则OA=OB,
∴△AOB是等腰三角形;
(2)根据图象可以得到:当y1>y2时x<3;
(3)设OC=x,则![]() x×4=8,解得:x=4,
x×4=8,解得:x=4,
则C的坐标是:(-4,0)或(4,0).
设直线AB的解析式是:y=kx+b,当C的坐标是:(-4,0)时,根据题意得:
![]() ,
,
解得: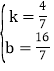 ,
,
则直线的解析式是:y=![]() x+
x+![]() ;
;
当C的坐标是(4,0)时,根据题意得:
![]() ,
,
解得:![]() ,
,
则直线的解析式是:y=-4x+16;
(4)把(3,4)代入y1=k1x得到:3k1=4,
解得:k1=![]() ,
,
当OA是底边时,OA的中点是(![]() ,2),设过OA的中点且与OA垂直的直线的解析式是:y=-
,2),设过OA的中点且与OA垂直的直线的解析式是:y=-![]() x+b,
x+b,
根据题意得:b=![]() ,
,
直线的解析式是:y=-![]() x+
x+![]() ,
,
当y=0时,x=![]() ,
,
则P的坐标是(![]() ,0);
,0);
当OA是腰,O是顶角的顶点时,OP=OA=5,则P的坐标是(5,0)或(-5,0);
当OA是腰,A是顶角的顶点时,AP=AO,则P与O关于x=3对称,则P的坐标是(6,0).
则P的坐标是:(![]() ,0)或(5,0)或(-5,0)或(6,0).
,0)或(5,0)或(-5,0)或(6,0).

【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如下表和图①:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
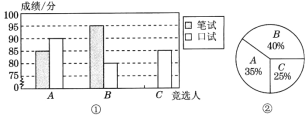
(1)请将表格和图①中的空缺部分补充完整;
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图②(没有弃权票,每名学生只能推荐一人),请计算每人的得票数;
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4∶3∶3的比确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.