题目内容
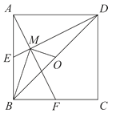
【题目】如图，在□ABCD中，BE⊥AD于点E，BF⊥CD于点F，AC与BE、BF分别交于点G，H。
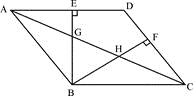
（1）求证：△BAE∽△BCF
（2）若BG＝BH，求证四边形ABCD是菱形
【答案】（1）略
（2）略
【解析】
证明（1）∵BE⊥AD，BF⊥CD
∴∠BEA＝∠BFC＝90° ………………（1＇）
又ABCD是平行四边形，
∴∠BAE＝∠BCF ……………………（2＇）
∴△BAE∽△BCF …………………………………………（3＇）
（2）∵△BAE∽△BCF
∴∠1＝∠2 ……………………………………………（4＇）
又BG＝BH ∴∠3＝∠4
∴∠BGA＝∠BHC ………………………………………………（5＇）
∴△BGA≌△BHC（ASA） ……………………………………（6＇）
∴AB＝BC ……………………………………………………（7＇）
∴□ABCD为菱形……………………………………………（8＇）
练习册系列答案
名校课堂系列答案
相关题目
