题目内容
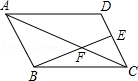
如图,在等腰梯形ABCD中,DC∥AB,E是DC延长线上的点,连接AE,交BC于点F。
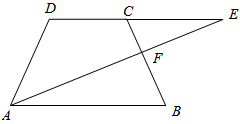
(1)求证:△ABF∽△ECF
(2)如果AD=5cm,AB=8cm,CF=2cm,求CE的长。

(1)求证:△ABF∽△ECF
(2)如果AD=5cm,AB=8cm,CF=2cm,求CE的长。
解:(1)证明:∵DC∥AB,∴∠B=∠ECF,∠BAF=∠E,
∴△ABF∽△ECF。
(2)∵在等腰梯形ABCD中,AD=BC, AD=5cm,AB=8cm,CF=2cm,∴BF=3cm。
∵△ABF∽△ECF,∴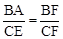 ,即
,即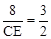 。
。
∴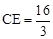 (cm)。
(cm)。
∴△ABF∽△ECF。
(2)∵在等腰梯形ABCD中,AD=BC, AD=5cm,AB=8cm,CF=2cm,∴BF=3cm。
∵△ABF∽△ECF,∴
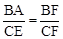 ,即
,即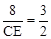 。
。∴
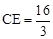 (cm)。
(cm)。试题分析:(1)由DC∥AB,即可证得△ABF∽△ECF。
(2)由△ABF∽△ECF得对应边成比例,根据比例式即可求得CE的长。

练习册系列答案
相关题目
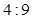 ,则在这两个三角形中,面积较小的三角形与面积较大的三角形的周长之比为 .
,则在这两个三角形中,面积较小的三角形与面积较大的三角形的周长之比为 .
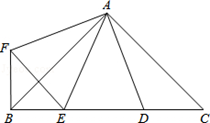
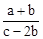 的值是
的值是