题目内容
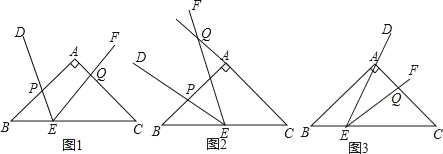
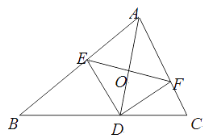
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④ AE2+DF2=AF2+DE2.上述结论中正确的是( )
A. ②③ B. ②④ C. ①②③ D. ②③④
【答案】D
【解析】
由AD是角平分线及DE、DF均为高可知△AED≌△AFD,则可得AE=AF,DE=DF,继而得到AD是EF的垂直平分线,由此可判断②和③正误,再由勾股定理可判断④的正误,而①的结论无法由已知条件推出.
解:∵AD是角平分线,
∴∠EAD=∠FAD,
∵∠AED=∠AFD=90°,AD=AD,
∴△ADE≌△AFD,
∴AE=AF,DE=DF,
∴AD⊥EF,②正确,
∵∠BAC=90°,∠AED=∠AFD=90°
又∵AE=AF,
∴四边形AEDF是正方形,③正确,
∵∠AED=∠AFD=90°,
∴AE2+DE2=AF2+DF2=AD2
∵DE=DF,
∴AE2+DF2=AF2+DE2,④正确.
根据前述已得结论,需要四边形AEDF是菱形才能得到OA=OD的结论,而题干并未给出这个条件,①错误,
故选择D.

练习册系列答案
相关题目