题目内容
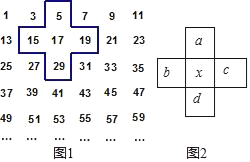
【题目】1952个正整数1,2,3,4,…,1952按如图方式排列成一个表:
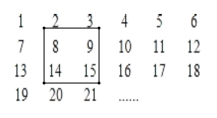
(1)如图,用一正方形方框任意框住4个数,记左上角的一个数为x,当被框住的4个数之和等于358时,x的值为多少?
(2)如(1)中方式,能否框住这样的4个数,它们的和等于2438?若能,则求出x的值;若不能,则说明理由.
(3)从左到右,第1到第6列各列数之和分别记为a1,a2,a3,a4,a5,a6,则这6个数中,最大数与最小数之差等于 .(直接填出结果,不写计算过程)
【答案】(1)86;(2)不能,理由见解析;(3)1627.
【解析】
(1)由正方形框可知,每行以6为循环,所以横向相邻两个数之间相差1,竖向两个数之间相差6,用含x的式子表示出框住的四个数,根据题意得到关于x的方程,解方程即可得;
(2)用含x的式子表示出框住的四个数,根据题意得到关于x的方程,解方程后进行判断即可;
(3)先确定出1952在哪一行哪一列,根据题意可知如果数字正好排成n行6列,则后面一列的数之和比前一列数之和大n ,据此确定出哪列数之和最大,哪列数之和最小即可求得答案.
(1)记左上角的一个数为x,则另外三个数用含x的式子表示出来,从小到大依次是x+1,x+6,x+7,
则x+(x+1)+(x+6)+(x+7)=358,
解得:x=86,
答:x的值为86;
(2)不能,理由如下:
∵x+(x+1)+(x+6)+(x+7)=2438时,
x=606,左上角的数不能是6的倍数,
∴它们的和不能等于2438;
(3)1952÷6=325…2,
∴1952在第326行第2列,
∴排到1950时,共排了325行,6列,后面的每一列数之和都比前一列数之和大325,
第6列比第1列大325×5=1625,
排到1952时,此时第1列、第2列有数字326个,其余各列仍然是325个数字,
此时第1列数之和比第6列数之和大1951-1625=326,
第2列数之和比第1列数之和大326,
∴a2最大,a3最小,
∴最大数与最小数之差=1952-325=1627,
故答案为:1627.