题目内容
【题目】操作:![]() 和
和![]() 都是等边三角形,
都是等边三角形,![]() 绕着
绕着![]() 点按顺时针方向旋转,
点按顺时针方向旋转,![]() 是
是![]() 、
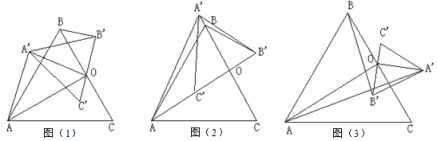
、![]() 的中点,有以下三种图形.
的中点,有以下三种图形.
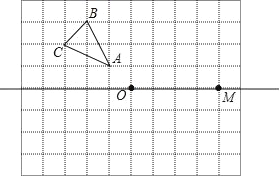
探究:
(1)在上述三个图形中,![]() 是否一个固定的值,若是,请选择任意一个图形求出这个比值;
是否一个固定的值,若是,请选择任意一个图形求出这个比值;
(2)![]() 的值是否也等于这个定值,若是,请结合图(1)证明你的结论;
的值是否也等于这个定值,若是,请结合图(1)证明你的结论;
(3)![]() 与
与![]() 有怎样的位置关系,请你结合图(2)或图(3)证明你的结论.
有怎样的位置关系,请你结合图(2)或图(3)证明你的结论.
【答案】(1)![]() 是一个固定的值,
是一个固定的值,![]() ,证明见解析;(2)
,证明见解析;(2)![]() 的值是等于这个定值,
的值是等于这个定值,![]() 证明见解析;(3)
证明见解析;(3)![]() 证明见解析.
证明见解析.
【解析】
(1)由等边三角形的性质可得AO⊥BC,BO=![]() BC=
BC=![]() AB,根据勾股定理计算即可求得AO=
AB,根据勾股定理计算即可求得AO=![]() BO,即AO∶BO是一个固定的值
BO,即AO∶BO是一个固定的值![]() ∶1;
∶1;
(2)由等边三角形的性质可得AO⊥BC,![]() ,由同角的余角相等可得
,由同角的余角相等可得![]() ,由(1)可得
,由(1)可得![]() ,可得
,可得![]() ,根据相似三角形的性质可得
,根据相似三角形的性质可得![]() ;
;
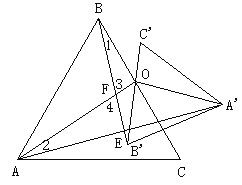
(3)在图(3)中,由(2)得![]() ,根据相似三角形的性质可得∠1=∠2,根据对顶角相等得∠3=∠4,则∠2+∠4=∠1+∠3=∠AOB=90°,即
,根据相似三角形的性质可得∠1=∠2,根据对顶角相等得∠3=∠4,则∠2+∠4=∠1+∠3=∠AOB=90°,即![]() .
.
(1)解:∵![]() 是等边三角形,由图(1)得AO⊥BC,
是等边三角形,由图(1)得AO⊥BC,![]()
∴![]() ,∴
,∴![]() ;
;
(2)证明:![]() ,
,![]()
![]() ,
,
∴![]()
∴![]()
∴![]()
(3)证明:在图(3)中,由(2)得![]()
∴![]() ,
,
∴∠2+∠4=∠1+∠3,即∠AEF =∠AOB
∵∠AOB=90°,
∴![]()
∴![]() .
.
故答案为:(1)![]() 是一个固定的值,
是一个固定的值,![]() ,证明见解析;(2)
,证明见解析;(2)![]() 的值是等于这个定值,
的值是等于这个定值,![]() 证明见解析;(3)
证明见解析;(3)![]() 证明见解析.
证明见解析.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目