题目内容
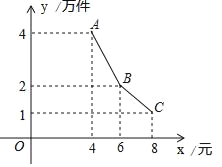
【题目】为了支持大学生创业，某市政府出台了一项优惠政策：提供10万元的无息创业贷款．小王利用这笔贷款，注册了一家淘宝网店，招收5名员工，销售一种火爆的电子产品，并约定用该网店经营的利润，逐月偿还这笔无息贷款．已知该产品的成本为每件4元，员工每人每月的工资为4千元，该网店还需每月支付其它费用1万元．该产品每月销售量y（万件）与销售单价x（元）万件之间的函数关系如图所示．
（1）求该网店每月利润w（万元）与销售单价x（元）之间的函数表达式；
（2）小王自网店开业起，最快在第几个月可还清10万元的无息贷款？
【答案】（1）当4≤x≤6时，w1=﹣x2+12x﹣35，当6≤x≤8时，w2=﹣
x2+7x﹣23；（2）最快在第7个月可还清10万元的无息贷款．
【解析】（1）y（万件）与销售单价x是分段函数，根据待定系数法分别求直线AB和BC的解析式，又分两种情况，根据利润=（售价﹣成本）×销售量﹣费用，得结论；
（2）分别计算两个利润的最大值，比较可得出利润的最大值，最后计算时间即可求解．
（1）设直线AB的解析式为：y=kx+b，
代入A（4，4），B（6，2）得：
，
解得：
，
∴直线AB的解析式为：y=﹣x+8，
同理代入B（6，2），C（8，1）可得直线BC的解析式为：y=﹣x+5，
∵工资及其他费作为：0.4×5+1=3万元，
∴当4≤x≤6时，w1=（x﹣4）（﹣x+8）﹣3=﹣x2+12x﹣35，
当6≤x≤8时，w2=（x﹣4）（﹣x+5）﹣3=﹣x2+7x﹣23；
（2）当4≤x≤6时，
w1=﹣x2+12x﹣35=﹣（x﹣6）2+1，
∴当x=6时，w1取最大值是1，
当6≤x≤8时，
w2=﹣x2+7x﹣23=﹣（x﹣7）2+
，
当x=7时，w2取最大值是1.5，
∴
=
=6
，
即最快在第7个月可还清10万元的无息贷款．
