题目内容
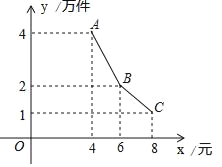
【题目】如图，在平面直角坐标系中，抛物线y=
x2﹣x﹣4与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．
（1）求点A，B，C的坐标；
（2）点P从A点出发，在线段AB上以每秒2个单位长度的速度向B点运动，同时，点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，当其中一个点到达终点时，另一个点也停止运动．设运动时间为t秒，求运动时间t为多少秒时，△PBQ的面积S最大，并求出其最大面积；
（3）在（2）的条件下，当△PBQ面积最大时，在BC下方的抛物线上是否存在点M，使△BMC的面积是△PBQ面积的1.6倍？若存在，求点M的坐标；若不存在，请说明理由．
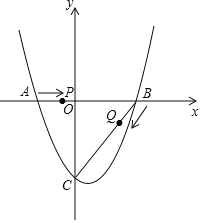
【答案】（1）点A的坐标为（﹣2，0），点B的坐标为（3，0），点C的坐标为（0，﹣4）；（2）当t=
时，△PBQ的面积取最大值，最大值为；（3）点M的坐标为（1，﹣4）或（2，﹣
）．
【解析】（1）代入x=0可求出点C的纵坐标，代入y=0可求出点A、B的横坐标，此题得解；
（2）根据点B、C的坐标，利用待定系数法可求出直线BC的解析式，过点Q作QE∥y轴，交x轴于点E，当运动时间为t秒时，点P的坐标为（2t-2，0），点Q的坐标为（3-
t，-
t），进而可得出PB、QE的长度，利用三角形的面积公式可得出S△PBQ关于t的函数关系式，利用二次函数的性质即可解决最值问题；
（3）根据（2）的结论找出点P、Q的坐标，假设存在，设点M的坐标为（m，
m2-m-4），则点F的坐标为（m，
m-4），进而可得出MF的长度，利用三角形的面积结合△BMC的面积是△PBQ面积的1.6倍，可得出关于m的一元二次方程，解之即可得出结论．
（1）当x=0时，y=x2﹣x﹣4=﹣4，
∴点C的坐标为（0，﹣4）；
当y=0时，有x2﹣x﹣4=0，
解得：x1=﹣2，x2=3，
∴点A的坐标为（﹣2，0），点B的坐标为（3，0）．
（2）设直线BC的解析式为y=kx+b（k≠0），
将B（3，0）、C（0，﹣4）代入y=kx+b，
，解得：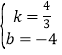
，
∴直线BC的解析式为y=x﹣4．
过点Q作QE∥y轴，交x轴于点E，如图1所示，
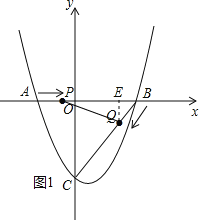
当运动时间为t秒时，点P的坐标为（2t﹣2，0），点Q的坐标为（3﹣t，﹣t），
∴PB=3﹣（2t﹣2）=5﹣2t，QE=t，
∴S△PBQ=
PBQE=﹣t2+2t=﹣（t﹣）2+．
∵﹣＜0，
∴当t=时，△PBQ的面积取最大值，最大值为．
（3）当△PBQ面积最大时，t=，
此时点P的坐标为（，0），点Q的坐标为（
，﹣1）．
假设存在，设点M的坐标为（m，m2﹣m﹣4），则点F的坐标为（m，m﹣4），
∴MF=m﹣4﹣（m2﹣m﹣4）=﹣m2+2m，
∴S△BMC=MFOB=﹣m2+3m．
∵△BMC的面积是△PBQ面积的1.6倍，
∴﹣m2+3m=×1.6，即m2﹣3m+2=0，
解得：m1=1，m2=2．
∵0＜m＜3，
∴在BC下方的抛物线上存在点M，使△BMC的面积是△PBQ面积的1.6倍，点M的坐标为（1，﹣4）或（2，﹣）．
