题目内容
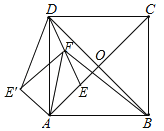
【题目】如图,正方形ABCD中,对角线AC、BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF、BF、E′F.若AE=2![]() .则四边形ABFE′的面积是_____.
.则四边形ABFE′的面积是_____.
【答案】12+4![]() .
.
【解析】
连接EB、EE′,作EM⊥AB于M,EE′交AD于N.易知△AEB≌△AED≌△ADE′,先求出正方形AMEN的边长,再求出AB,根据S四边形ABFE′=S四边形AEFE′+S△AEB+S△EFB即可解决问题.
连接EB、EE′,作EM⊥AB于M,EE′交AD于N,如图所示:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,AC⊥BD,AO=OB=OD=OC,
∠DAC=∠CAB=∠DAE′=45°,
在△ADE和△ABE中,
 ,
,
∴△ADE≌△ABE(SAS),
∵把△ADE沿AD翻折,得到△ADE′,
∴△ADE≌△ADE′≌△ABE,
∴DE=DE′,AE=AE′,
∴AD垂直平分EE′,
∴EN=NE′,
∵∠NAE=∠NEA=∠MAE=∠MEA=45°,AE=2![]() ,
,
∴AM=EM=EN=AN=2,
∵ED平分∠ADO,EN⊥DA,EO⊥DB,
∴EN=EO=2,AO=2+2![]() ,
,
∴AB=![]() AO=4+2
AO=4+2![]() ,
,
∴S△AEB=S△AED=S△ADE′=![]() ×2×(4+2
×2×(4+2![]() )=4+2
)=4+2![]() ,S△BDE=S△ADB﹣2S△AEB=
,S△BDE=S△ADB﹣2S△AEB=![]() ×(4+2
×(4+2![]() )2﹣2×
)2﹣2×![]() ×2×(4+2
×2×(4+2![]() )=4,
)=4,
∵DF=EF,
∴S△EFB=![]() S△BDE=
S△BDE=![]() ×4=2,
×4=2,
∴S△DEE′=2S△AED﹣S△AEE′=2×(4+2![]() )﹣
)﹣![]() ×(2
×(2![]() )2=4+4
)2=4+4![]() ,S△DFE′=
,S△DFE′=![]() S△DEE′=
S△DEE′=![]() ×(4+4
×(4+4![]() )=2+2
)=2+2![]() ,
,
∴S四边形AEFE′=2S△AED﹣S△DFE′=2×(4+2![]() )﹣(2+2
)﹣(2+2![]() )=6+2
)=6+2![]() ,
,
∴S四边形ABFE′=S四边形AEFE′+S△AEB+S△EFB=6+2![]() +4+2
+4+2![]() +2=12+4
+2=12+4![]() ;
;
故答案为:12+4![]() .
.


【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?