题目内容
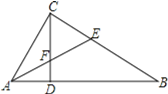
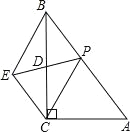
【题目】如图,在△ABC中,∠ACB=90°,AC=15.sin∠A=![]() ,点D是BC的中点,点P是AB上一动点(不与点B重合),延长PD至E,使DE=PD,连接EB、EC.
,点D是BC的中点,点P是AB上一动点(不与点B重合),延长PD至E,使DE=PD,连接EB、EC.
(1)求证;四边形PBEC是平行四边形;
(2)填空:
①当AP的值为 时,四边形PBEC是矩形;
②当AP的值为 时,四边形PBEC是菱形.
【答案】证明见解析;(2)①9;②12.5.
【解析】
(1)根据对角线互相平分的四边形为平行四边形证明即可;
(2)①若四边形PBEC是矩形,则∠APC=90°,求得AP即可;
②若四边形PBEC是菱形,则CP=PB,求得AP即可.
∵点D是BC的中点,∴BD=CD.
∵DE=PD,∴四边形PBEC是平行四边形;
(2)①当∠APC=90°时,四边形PBEC是矩形.
∵AC=15.sin∠A=![]() ,∴PC=12,由勾股定理得:AP=9,∴当AP的值为9时,四边形PBEC是矩形;
,∴PC=12,由勾股定理得:AP=9,∴当AP的值为9时,四边形PBEC是矩形;
②在△ABC中,∵∠ACB=90°,AC=15.sin∠A=![]() ,所以设BC=4x,AB=5x,则(4x)2+152=(5x)2,解得:x=5,∴AB=5x=25.
,所以设BC=4x,AB=5x,则(4x)2+152=(5x)2,解得:x=5,∴AB=5x=25.
当PC=PB时,四边形PBEC是菱形,此时点P为AB的中点,所以AP=12.5,∴当AP的值为12.5时,四边形PBEC是菱形.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目