Question

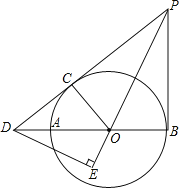
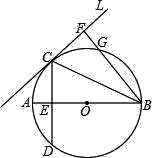
【题目】如图，已知AB是⊙O的直径，直线l与⊙O相切于点C且，弦CD交AB于E，BF⊥l，垂足为F，BF交⊙O于G．

（1）求证：CE2=FGFB；

（2）若tan∠CBF=，AE=3，求⊙O的直径．

Answer 1

【答案】（1）见解析;（2）15．

【解析】

（1）由切割线定理知：CF2=FGFB，欲证本题的结论，需先证得CE=CF；可通过证△BCE≌△BCF得出；

（2）欲求⊙O的直径，已知AE的长，关键是求出BE的长度；在Rt△ABC中，CE⊥AB，根据射影定理得到CE2=AEEB，由此可求出BE的长．

（1）连接AC，

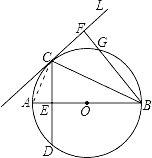
∵AB为直径，

∴∠ACB=90°，

∵，且AB是直径，

∴AB⊥CD，

即CE是Rt△ABC的高，

∴∠A=∠ECB，∠ACE=∠EBC，

∵CF是⊙O的切线，

∴∠FCB=∠A，CF2=FGFB，

∴∠FCB=∠ECB，

∵∠BFC=∠CEB=90°，CB=CB，

∴△BCF≌△BCE，

∴CE=CF，∠FBC=∠CBE，

∴CE2=FGFB；

（2）∵∠CBF=∠CBE，∠CBE=∠ACE，

∴∠ACE=∠CBF；

∴tan∠CBF=tan∠ACE=，

∵AE=3，

∴，

∴CE=6，

在Rt△ABC中，CE是高，

∴CE2=AEEB，即62=3EB，

∴EB=12，

∴⊙O的直径为：12+3=15．