题目内容
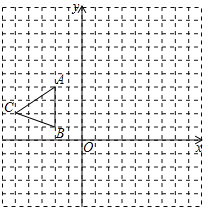
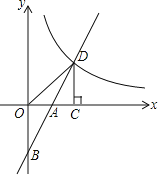
【题目】如图，在平面直角坐标系中，直线
与坐标轴交于
两点，与反比例函数
的图象交于
点，过点作
轴，垂足为
，连接
．已知
．
（1）如果
，求
的值；
（2）试探究与
的数量关系．
【答案】（1）16；（2）
．
【解析】
（1）首先求出直线
与坐标轴交点的坐标，然后由△AOB≌△ACD得到CD=OB，AO=AC，即可求出D坐标，由点D在双曲线
的图象上求出k的值；
（2）首先直线y=2x+b与坐标轴交点的坐标为
，
，再根据△AOB≌△ACD得到CD=OB，AO=AC，即可求出D坐标，把D点坐标代入反比例函数解析式求出k和b之间的关系．
（1）当
时，
直线与坐标轴交点的坐标为：
，
．
，
，
，
∴点
的坐标为
．
点在双曲线的图象上，
（2）直线
与坐标轴交点的坐标为，．
，
，，
∴点的坐标为
．
点在双曲线的图象上，
．
即
与
的数量关系为：．
练习册系列答案
相关题目
