题目内容
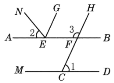
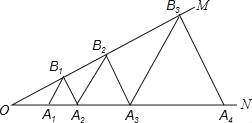
【题目】如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=1,则△A9B9A10的边长为( )
A. 32 B. 64 C. 128 D. 256
【答案】D
【解析】
据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2…进而得出答案.
如图,
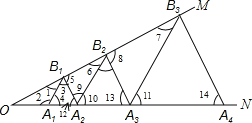
∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°-120°-30°=30°,
又∵∠3=60°,
∴∠5=180°-60°-30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
…
∴△AnBnAn+1的边长为 2n-1,
∴△A9B9A10的边长为29-1=28=256.
故选D.

【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?