题目内容
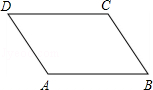
如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得AG=DE+HG,连接BH.求证:∠ABH=∠CDE.


证明见解析
试题分析:根据正方形的性质可得AB=AD,∠ABG=∠DAF=90°,再根据同角的余角相等求出∠1=∠2,然后利用“角边角”证明△ABG和△DAF全等,根据全等三角形对应边相等可AF=BG,AG=DF,全等三角形对应角相等可得∠AFD=∠BGA,然后求出EF=HG,再利用“边角边”证明△AEF和△BHG全等,根据全等三角形对应角相等可得∠1=∠3,从而得到∠2=∠3,最后根据等角的余角相等证明即可。
证明:在正方形ABCD中,AB=AD,∠ABG=∠DAF=90°,

∵DE⊥AG,∴∠2+∠EAD=90°。
又∵∠1+∠EAD=90°,∴∠1=∠2。
在△ABG和△DAF中,
∵∠1=∠2,AB=AD,∠ABG=∠DAF=90°,
∴△ABG≌△DAF(ASA)。
∴AF=BG,AG=DF,∠AFD=∠BGA。
∵AG=DE+HG,AG=DE+EF,∴EF=HG。
在△AEF和△BHG中,∵AF=BG,∠AFD=∠BGA,EF=HG,
∴△AEF≌△BHG(SAS),∴∠1=∠3。∴∠2=∠3。
∵∠2+∠CDE=∠ADC=90°,∠3+∠ABH=∠ABC=90°,∴∠ABH=∠CDE。

练习册系列答案
相关题目





 ,则线段EH的长为 .
,则线段EH的长为 .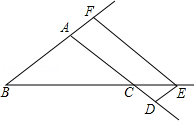

 ABCD中,下列结论一定正确的是
ABCD中,下列结论一定正确的是