Question

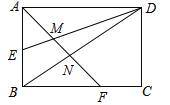
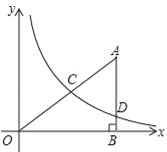
【题目】如图1，点E是正方形ABCD的边CD上一点（不与C、D重合），连接AE，过点A作AF⊥AE交CB的延长线于点F

（1）求证：AE=AF；

（2）连接EF，N为EF之中点，连接BN，求的值；

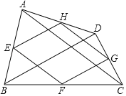
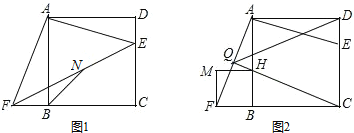
（3）以BF为边作正方形BFMH，如图2，CH与AF相交于点Q，当E在CD上运动（不与C、D重合），问∠CQD的大小是否发生变化？若不变，求其值；若变化，请指出其范围．

Answer 1

【答案】（1）见解析；（2）；（3）不变，45°.

【解析】

（1）由四边形ABCD是正方形，得到AB=AD，∠ABC=∠BAD=∠D=90°，∠ABF=90°，因为∠FAE=90°，所以∠FAE-∠BAE=∠BAD-∠BAE，即；∠FAB=∠EAD，得到△ABF≌△DAE，求出AF=AE；
（2）取FC的中点N，连接MN，AM，因为点M是FE的中点，得到CE=2MN，由∠AKM=∠FKB，∠AMF=∠MNB=90°，得到△AKM∽△BKM，，因为∠AKB∠=MKB，所以△AFK∽△BKF，得到∠KBM=∠AFK=45°，∠MBN=45°，所以BM=MN，；
（3）过点D作DQ⊥PD交PC的延长线于Q，由四边形BFHG是正方形，得到BG=BF，所以△ABF≌△CBG，∠FAB=∠BCG，由∠AGP=∠CGB，得到∠APG=∠ABC=90°，因为∠ADC=∠PDQ=90°，得到∠ADP=∠QDC，由AB∥CD，得到∠DCQ=∠AGC，∠PAG+∠BAD=∠PAG+∠APG，即∠PAD=∠AGC=∠DCQ，得到△PAD≌△QCD（ASA），PD=DQ，∠DPQ=45°，得出∠APD=45°．

（1）证明：∵AF⊥AE，∠BAD=90°，

∴∠FAB=∠EAD，

在△FAB和△EAD中，

，

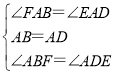∴△FAB≌△EAD，

∴AE=AF；

（2）如图1，连接AN，作NM⊥BC于M，则NM∥CD，

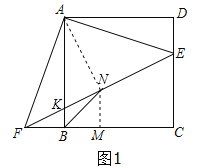
又点N是FE的中点，

∴CE=2MN，

∵∠AKN=∠FKB，∠ANK=∠FBK=90°，

∴△AKN∽△FKB，

∴，

又∠AKF=∠NKB，

∴△AKF∽△NKB，

∴∠NBK=∠AFK=45°，

∴∠NBM=45°，

∴BN=MN，

∴；

（3）如图2，过点D作DR⊥QD交BC的延长线于R，

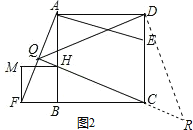
∵四边形BFMH是正方形，

∴BH=BF，

在△ABF与△CBH中，

，

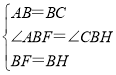∴△ABF≌△CBH，

∴∠BAF=∠BCH，又∠AHQ=∠CHB，

∴∠AQH=∠ABC=90°，

∵∠AHC=∠AQH+∠BAF，∠QAD=∠BAF+∠BAD，

∴∠AHC=∠QAD，

∵AB∥CD，

∴∠AHC=∠DCR，

∴∠DCR=∠QAD，

∵∠ADC=∠QDR=90°，

∴∠ADQ=∠CDR，

在△QAD和△DCR中，

，

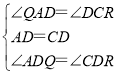∴△QAD≌△RCD，

∴DQ=DR，

∴∠CQD=45°．