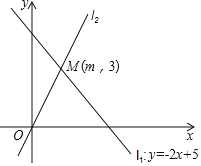题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于A,B两点(点B在点A的左侧),与y轴交于点C,顶点为D,其对称轴与
轴交于A,B两点(点B在点A的左侧),与y轴交于点C,顶点为D,其对称轴与![]() 轴交于点E,联接AD,OD.
轴交于点E,联接AD,OD.
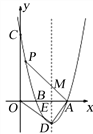
(1)求顶点D的坐标(用含![]() 的式子表示);
的式子表示);
(2)若OD⊥AD,求该抛物线的函数表达式;
(3)在(2)的条件下,设动点P在对称轴左侧该抛物线上,PA与对称轴交于点M,若△AME与△OAD相似,求点P的坐标.
【答案】(1)(4,-4m)(2)![]() (3)(0,
(3)(0,![]() )或(1,
)或(1,![]() )
)
【解析】分析:(1)、将已知的二次函数进行配方,从而得出顶点坐标;(2)、将二次函数转化为交点式,从而得出点A和点B的坐标,根据勾股定理以及OD⊥AD得出等量关系,求出m的值;(3)、过点P作PH⊥x轴于点H,则△APH∽△AME,首先设出点P的坐标,根据△APH∽△AME∽△AOD和△APH∽△AME∽△OAD时分别得出答案.
详解:(1)∵![]() , ∴顶点D的坐标为(4,-4m).
, ∴顶点D的坐标为(4,-4m).
(2)∵![]()
∴点A(6,0),点B(2,0),则OA=6, ∵抛物线的对称轴为x=4,∴点E(4,0),
则OE=4,AE=2, 又DE=4m,
∴由勾股定理得:![]() ,
, ![]() ,
,
又OD⊥AD,∴![]() , 则
, 则![]() ,解得:
,解得:![]() ,
,
∵m>0,∴抛物线的函数表达式![]() .
.
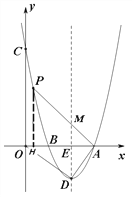
(3)如图,过点P作PH⊥x轴于点H,则△APH∽△AME,
在Rt△OAD中,![]() , 设点P的坐标为
, 设点P的坐标为![]() ,
,
当△APH∽△AME∽△AOD时,∵![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:x=0,x=6(舍去),∴点P的坐标为![]() ;
;
②△APH∽△AME∽△OAD时,∵![]() , ∴
, ∴![]() ,即
,即![]() ,
,
解得:x=1,x=6(舍去),∴点P的坐标为![]() ;
;
综上所述,点P的坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目