题目内容
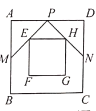
【题目】已知四边形ABCD是个边长为2a的正方形,P、M、N分别是边AD、AB、CD的中点,E、H分别是PM、PN的中点,则正方形EFGH的面积是( )
A.![]() B.
B.![]() C.a2D.2a2
C.a2D.2a2
【答案】C
【解析】
先连接MN,由于四边形ABCD是正方形,易得AB=CD,AB∥CD,∠A=90°,而M、N是AB、CD的中点,易知AM=![]() AB,DN=
AB,DN=![]() CD,那么AM平行等于DN,而∠A=90°,易证四边形AMND是矩形,从而有MN=AD,在△PMN中,E、H是PM、PN的中点,可知EH是△PMN的中位线,根据三角形中位线定理可得EH=
CD,那么AM平行等于DN,而∠A=90°,易证四边形AMND是矩形,从而有MN=AD,在△PMN中,E、H是PM、PN的中点,可知EH是△PMN的中位线,根据三角形中位线定理可得EH=![]() MN=a,那么就可求出正方形EFGH的面积.
MN=a,那么就可求出正方形EFGH的面积.
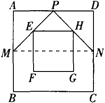
解:如右图所示,连接MN,
∵四边形ABCD是正方形,
∴AB=CD,AB∥CD,∠A=90°,
又∵M、N是AB、CD的中点,
∴AM=![]() AB,DN=
AB,DN=![]() CD,
CD,
∴AM=DN,AM∥DN,
又∵∠A=90°,
∴四边形AMND是矩形,
∴MN=AD=2a,
∵E、H是PM、PN的中点,
∴EH是△PMN的中位线,
∴EH=![]() MN=a,
MN=a,
∴S正方形EFGH=a2.
故选:C.

练习册系列答案
相关题目