题目内容
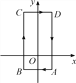
【题目】如图所示,在矩形![]() 中,
中,![]() ,点
,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 的速度移动,如果点
的速度移动,如果点![]() 同时出发,用
同时出发,用![]() 表示移动的时间(
表示移动的时间(![]() ).
).
(1)当![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(2)求四边形![]() 的面积,并探索一个与计算结果有关的结论.
的面积,并探索一个与计算结果有关的结论.
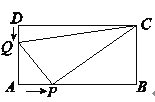
【答案】(1)当![]() 时,
时,![]() 为等腰三角形;(2)
为等腰三角形;(2)![]()
![]() ,结论:四边形
,结论:四边形![]() 的面积始终不变,为36
的面积始终不变,为36![]() .
.
【解析】
(1)若△QAP为等腰直角三角形,则只需AQ=AP,列出等式6-t=2t,解得t的值即可,
(2)四边形QAPC的面积=矩形ABCD的面积-三角形CDQ的面积-三角形PBC的面积,设DQ=x.根据题干条件可得四边形QAPC的面积=72-![]() x12-
x12-![]() ×6×(12-2x)=72-36=36,故可得结论四边形QAPC的面积是矩形ABCD面积的一半.
×6×(12-2x)=72-36=36,故可得结论四边形QAPC的面积是矩形ABCD面积的一半.
(1)由![]() ,得
,得![]() .若
.若![]() 为等腰三角形,则只能是
为等腰三角形,则只能是![]() .故当
.故当![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
(2)![]()
![]() .
.
结论:四边形![]() 的面积始终不变,为36
的面积始终不变,为36![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目