ΧβΡΩΡΎ»ί
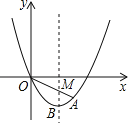
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§œΏΕΈABΒΡΝΫΗωΕΥΒψAΘ®0Θ§2Θ©Θ§BΘ®1Θ§0Θ©Θ§ΒψCΈΣœΏΕΈABΒΡ÷–ΒψΘ°ΫΪœΏΕΈBA»ΤΒψBΑ¥Υ≥ ±’κΖΫœρ–ΐΉΣ90ΓψΒΟΒΫœΏΕΈBDΘ§Ν§ΫαCDΘ§ADΘ°ΒψP «÷±œΏBD…œΒΡ“ΜΗωΕ·ΒψΘ°
Θ®1Θ©«σΒψDΒΡΉχ±ξΚΆ÷±œΏBDΒΡΫβΈω ΫΘΜ
Θ®2Θ©Β±ΓœPCDΘΫΓœADC ±Θ§«σΒψPΒΡΉχ±ξΘΜ
Θ®3Θ©»τΒψQ «Ψ≠ΙΐΒψBΘ§ΒψDΒΡ≈ΉΈοœΏyΘΫax2+bx+2…œΒΡ“ΜΗωΕ·ΒψΘ§«κΡψΧΫΥςΘΚ «Ζώ¥φ‘Ύ’β―υΒΡΒψQΘ§ ΙΒΟ“‘ΒψPΓΔΒψQΓΔΒψDΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςACDœύΥΤΘ°»τ¥φ‘ΎΘ§«κ«σ≥ωΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©ΒψPΒΡΉχ±ξΈΣΘ®2Θ§
ΘΜΘ®2Θ©ΒψPΒΡΉχ±ξΈΣΘ®2Θ§![]() Θ©ΜρΘ®8Θ§
Θ©ΜρΘ®8Θ§![]() Θ©ΘΜΘ®3Θ©ΦϊΫβΈω.
Θ©ΘΜΘ®3Θ©ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΉςDEΓΆx÷αΘ§ΙΙ‘λ»ΪΒ»»ΐΫ«–Έ«σΒψDΒΡΉχ±ξΘ§¥ΐΕ®œΒ ΐΖ®«σBDΒΡΫβΈω ΫΘΜ
Θ®2Θ©“ΣΧΊ±πΉΔ“βΓœPCDΘΫΓœADC”–ΝΫ÷÷«ιΩωΘΚΓœPCD‘Ύ÷±œΏCDΒΡœ¬ΖΫΜρ…œΖΫΘ§Ζά÷Ι¬©ΫβΘΜ
Θ®3Θ©ΗυΨίΓœPDQΖ÷±π”κΓœACDΘ§ΓœADCΘ§ΓœCADœύΒ»Ϋχ––Χ÷¬έΘ§ΟΩ÷÷«ι–ΈΕΦΜΙ“Σ‘ΌΖ÷ΝΫ÷÷«ιΩωΫχ––Ζ÷ΈωΘ§ΜΙ“ΣΉΔ“βΒψ‘ΎΒψDΒΡΉσ≤ύΚΆ”“≤ύΝΫ÷÷≤ΜΆ§«ιΩωΘ§“‘Ζά¬©ΫβΘ°
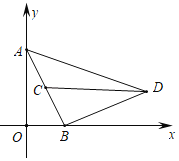
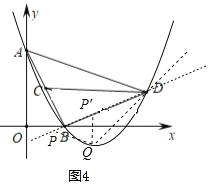
ΫβΘΚΘ®1Θ©»γΆΦ1Θ§ΙΐDΉςDEΓΆx÷α”ΎEΘ§”…–ΐΉΣΒΟΘΚBAΘΫBDΘ§ΓœABDΘΫ90ΓψΘ§
ΓΏDEΓΆx÷αΘ§
ΓύΓœBEDΘΫΓœAOBΘΫ90Γψ
ΓύΓœBAO+ΓœABOΘΫ90ΓψΘ§ΓœDBE+ΓœABOΘΫ90ΓψΘ§
ΓύΓœBAOΘΫΓœDBE
ΓύΓςBAOΓ’ΓςDBEΘ®AASΘ©
ΓύBEΘΫOAΘΫ2Θ§DEΘΫOBΘΫ1Θ§
ΓύOEΘΫOB+BEΘΫ1+2ΘΫ3
ΓύDΘ®3Θ§1Θ©ΘΜ
…η÷±œΏBDΒΡΫβΈω ΫΈΣyΘΫmx+nΘ§ΫΪBΘ®1Θ§0Θ©Θ§DΘ®3Θ§1Θ©Ζ÷±π¥ζ»κΒΟ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ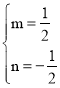 Θ§
Θ§
Γύ÷±œΏBDΒΡΫβΈω ΫΈΣ![]() Θ°
Θ°
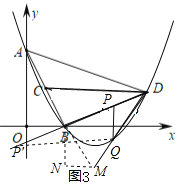
Θ®2Θ©»γΆΦ2Θ§ΓΏΓœPCDΘΫΓœADC
ΓύCPΓΈAD
Γύ![]() Θ§
Θ§
ΓΏBCΘΫCA
ΓύBPΘΫPD
ΓύPΘ®2Θ§![]() Θ©Θ§
Θ©Θ§
ΉςΒψPΙΊ”Ύ÷±œΏCDΒΡΕ‘≥ΤΒψPΓδΘ®2Θ§![]() Θ©Θ§Ν§Ϋ”CPΓδΘ§‘ρΓœPΓδCDΘΫΓœPCDΘΫΓœADC
Θ©Θ§Ν§Ϋ”CPΓδΘ§‘ρΓœPΓδCDΘΫΓœPCDΘΫΓœADC
…η÷±œΏCPΓδΒΡΫβΈω ΫΈΣyΘΫm1x+n1Θ§ΫΪCΘ®![]() Θ§1Θ©Θ§PΓδΘ®2Θ§
Θ§1Θ©Θ§PΓδΘ®2Θ§![]() Θ©¥ζ»κΒΟ
Θ©¥ζ»κΒΟ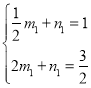 Θ§ΫβΒΟ
Θ§ΫβΒΟ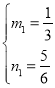 Θ§
Θ§
Γύ÷±œΏCPΓδΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
ΝΣΝΔΖΫ≥ΧΉι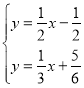 Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§ΓύPΘ®8Θ§
Θ§ΓύPΘ®8Θ§![]() Θ©Θ§
Θ©Θ§
Ήέ…œΥυ ωΘΚΒψPΒΡΉχ±ξΈΣΘ®2Θ§![]() Θ©ΜρΘ®8Θ§
Θ©ΜρΘ®8Θ§![]() Θ©Θ°
Θ©Θ°
Θ®3Θ©ΫΪBΘ®1Θ§0Θ©Θ§DΘ®3Θ§1Θ©Ζ÷±π¥ζ»κyΘΫax2+bx+2ΒΟ![]() Θ§
Θ§
ΫβΒΟ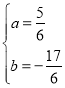 Θ§
Θ§
Γύ≈ΉΈοœΏΫβΈω ΫΈΣ![]() Θ§
Θ§
ΓςPDQ”κΓςACDœύΥΤΖ÷»ΐ÷÷«ιΩωΘΚ
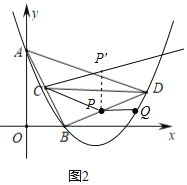
ΔΌ»γΆΦ3Θ§ΓœPDQΘΫΓœDACΘΫ45ΓψΘ§―”≥ΛAB÷ΝMΘ§ ΙBMΘΫBDΘ§Ν§Ϋ”DMΫΜ≈ΉΈοœΏ”ΎQΘ§
ΉςBNΓΈy÷αΘ§MNΓΈx÷αΫΜBN”ΎNΘ§
ΓύBMΘΫBDΘΫ![]() Θ§ΓœMBNΘΫΓœBAOΘ§ΓœBNMΘΫ90Γψ
Θ§ΓœMBNΘΫΓœBAOΘ§ΓœBNMΘΫ90Γψ
Γύ![]() ΘΫtanΓœMBNΘΫtanΓœBAOΘΫ
ΘΫtanΓœMBNΘΫtanΓœBAOΘΫ![]() Θ§
Θ§
ΓύMNΘΫ1Θ§BNΘΫ2Θ§
ΓύMΘ®2Θ§©¹2Θ©ΘΜ
…η÷±œΏDMΫβΈω ΫΈΣyΘΫm2x+n2Θ§ΫΪDΘ®3Θ§1Θ©ΓΔMΘ®©¹2Θ§©¹2Θ©¥ζ»κΘ§
ΒΟ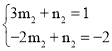 Θ§
Θ§
ΫβΒΟ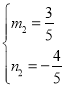
Γύ÷±œΏDMΫβΈω ΫΈΣ![]()
ΝΣΝΔΖΫ≥ΧΉι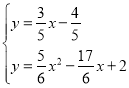 Θ§
Θ§
ΫβΒΟ![]() Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§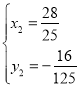
Q![]() ΘΜ
ΘΜ
»τΓœDPQΘΫΓœACDΘ§‘ρΩ…÷ΛΒΟPQΓΈy÷αΘ§
ΓύP1![]() Θ§
Θ§
»τΓœDPQΘΫΓœADCΘ§Ω…«σΒΟ
P2![]() Θ§
Θ§
ΔΎΓœPDQΘΫΓœADC ±Θ§
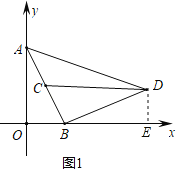
»γΆΦ4Θ§ΒψQΈΜ”Ύ÷±œΏBDœ¬ΖΫ ±Θ§
ΓœPDQ+ΓœCDBΘΫΓœADC+ΓœCDBΘ§Φ¥ΓœCDQΘΫΓœADBΘΫ45ΓψΘ§
ΓΏCDΓΈx÷αΘ§Γύ÷±œΏDQ”κx÷αΦ–Ϋ«ΈΣ45ΓψΘ§…ηDQΫβΈω ΫΈΣyΘΫx+kΘ§ΫΪDΘ®3Θ§1Θ©¥ζ»κΒΟ3+kΘΫ1Θ§kΘΫ©¹2
ΓύyΘΫx©¹2
ΝΣΝΔΖΫ≥ΧΉι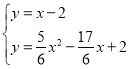 Θ§
Θ§
ΫβΒΟ![]() Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§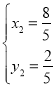 Θ§
Θ§
Γύ![]() Θ§
Θ§
“Ή«σ÷±œΏADΫβΈω ΫΈΣ![]() Θ§
Θ§
Γύ÷±œΏPQΫβΈω ΫΈΣ![]()
ΝΣΝΔΖΫ≥ΧΉι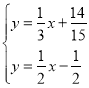 Θ§ΫβΒΟ
Θ§ΫβΒΟ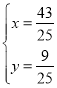 Θ§
Θ§
ΓύP3![]() Θ§
Θ§
»τΓœDPQΘΫΓœACDΘ§‘ρPQΓΈy÷αΘ§![]() ΘΜ
ΘΜ
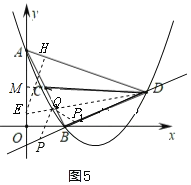
»γΆΦ5Θ§ΒψQΈΜ”Ύ÷±œΏBD…œΖΫ ±Θ§
‘Ύy÷α…œ»ΓΒψEΘ®0Θ§![]() Θ©Θ§―”≥ΛDCΫΜy÷α”ΎΒψMΘ§Ν§Ϋ”DEΫΜ≈ΉΈοœΏ”ΎQΘ§ΙΐΒψEΉςEHΓΆAD”ΎHΘ§
Θ©Θ§―”≥ΛDCΫΜy÷α”ΎΒψMΘ§Ν§Ϋ”DEΫΜ≈ΉΈοœΏ”ΎQΘ§ΙΐΒψEΉςEHΓΆAD”ΎHΘ§
ΉςΓœDQP1ΘΫ45ΓψΜρΓœDQPΘΫΓœACDΘ§ΒψPΘ§P1‘Ύ÷±œΏBD…œΘ§
‘ΎRtΓςAEH÷–Θ§tanΓœADM÷–Θ§tanΓœDAMΘΫ![]() ΘΫ3Θ§AMΘΫ1Θ§DMΘΫ3Θ§AMΘΫ
ΘΫ3Θ§AMΘΫ1Θ§DMΘΫ3Θ§AMΘΫ![]() ΘΜ
ΘΜ
‘ΎRtΓςAEH÷–Θ§tanΓœEADΘΫ![]() ΘΫ3Θ§AEΘΫAO©¹OEΘΫ2©¹
ΘΫ3Θ§AEΘΫAO©¹OEΘΫ2©¹![]() Θ§
Θ§
…ηAHΘΫxΘ§‘ρEHΘΫ3xΘ§
”…Ι¥Ι…Ε®άμΒΟ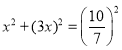 Θ§ΫβΒΟxΘΫ
Θ§ΫβΒΟxΘΫ![]() Θ§
Θ§
ΓύEHΘΫ![]() Θ§DHΘΫ
Θ§DHΘΫ![]()
ΓύtanΓœEDAΘΫ![]() ΘΫtanΓœBAC
ΘΫtanΓœBAC
ΓύΓœEDAΘΫΓœBAC
ΓύΓœBDQΘΫΓœADC
“Ή«σΒΟ÷±œΏDEΫβΈω ΫΈΣyΘΫ![]() Θ§Ω…ΝΣΝΔΖΫ≥ΧΉιΫβΒΟQ
Θ§Ω…ΝΣΝΔΖΫ≥ΧΉιΫβΒΟQ![]() ,
,
»τΓœDQPΘΫΓœDACΘΫ45ΓψΘ§“Ή«σΒΟDQΘΫ![]() Θ§
Θ§
”…ΓςADCΓΉΓςQDPΒΟ![]() Θ§
Θ§
ΓύDPΓΝDAΘΫDCΓΝDQΘ§Φ¥![]() Θ§
Θ§
ΓύDPΘΫ![]()
ΓύP5![]() Θ°
Θ°
»τΓœDPQΘΫΓœDACΘΫ45ΓψΘ§
”…ΓςDPQΓΉΓςDACΒΟ![]()
ΓύDPΓΝDCΘΫDAΓΝDQΘ§Φ¥DPΓΝ![]()
ΓύDPΘΫ![]()
ΓύP6![]()
Δέ»γΆΦ6Θ§ΓœPDQΘΫΓœACDΘ§
Β±ΒψP‘Ύ…δœΏDB…œ ±Θ§
ΓΏΓœACDΘΫΓœCDB+ΓœCBDΘΫΓœCDB+90Γψ
ΓύDQΓΆCD ±Θ§ΓœBDQΘΫΓœACDΘ§œ‘»ΜΘ§¥Υ ±ΒψQ≤Μ¥φ‘ΎΘ°
Β±ΒψP‘ΎDBΖ¥œρ―”≥ΛœΏ…œ ±Θ§
“Ή«σΒΟ÷±œΏDQΫβΈω ΫΈΣyΘΫ![]() ,
,
ΝΣΝΔΖΫ≥ΧΉιΩ…«σΒΟQ![]() Θ§
Θ§
ΓύDQΘΫ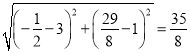
»τΓœPQDΘΫΓœADCΘ§‘ρΓςDPQΓΉΓςCAD
Γύ![]() Θ§Φ¥DPΓΝCDΘΫCAΓΝDQΘ§DPΓΝ
Θ§Φ¥DPΓΝCDΘΫCAΓΝDQΘ§DPΓΝ![]()
ΓύDPΘΫ![]()
ΓύP7![]() Θ§
Θ§
»τΓœPQDΘΫΓœDACΘ§‘ρΓςDPQΓΉΓςCDA
Γύ![]() Θ§Φ¥DPΓΝCAΘΫCDΓΝDQΘ§DPΓΝ
Θ§Φ¥DPΓΝCAΘΫCDΓΝDQΘ§DPΓΝ![]()
ΓύDPΘΫ![]()
ΓύP8![]()
Ήέ…œΥυ ωΘΚΖϊΚœ“Σ«σΒΡΒψPΒΡΉχ±ξΈΣP1![]() ,P2
,P2![]() Θ§P3
Θ§P3![]() Θ§
Θ§![]() ΘΜ P5
ΘΜ P5![]() Θ§P6
Θ§P6![]() Θ§P7
Θ§P7![]() Θ§P8
Θ§P8![]() Θ°
Θ°


 ΨΪ”ΔΩΎΥψΩ®œΒΝ–¥πΑΗ
ΨΪ”ΔΩΎΥψΩ®œΒΝ–¥πΑΗ ”Π”ΟΧβΒψ≤ΠœΒΝ–¥πΑΗ
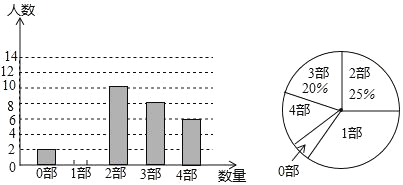
”Π”ΟΧβΒψ≤ΠœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΚλ–«ΙΪΥΨ…ζ≤ζΒΡΡ≥÷÷ ±Νν…ΧΤΖΟΩΦΰ≥…±ΨΈΣ20‘ΣΘ§Ψ≠Ιΐ –≥ΓΒς―–ΖΔœ÷Θ§’β÷÷…ΧΤΖ‘ΎΈ¥ά¥40ΧλΡΎΒΡ »’œζ έΝΩ(Φΰ)”κ ±Φδ(Χλ)ΒΡΙΊœΒ»γœ¬±μΘΚ
±Φδ(Χλ) | 1 | 3 | 6 | 10 | 36 | Γ≠ |
»’œζ έΝΩ(Φΰ) | 94 | 90 | 84 | 76 | 24 | Γ≠ |
Έ¥ά¥40ΧλΡΎΘ§«Α20ΧλΟΩΧλΒΡΦέΗώy1(‘Σ/Φΰ)”κt ±Φδ(Χλ)ΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚy1=![]() t+25(1ΓήtΓή20«“tΈΣ’ϊ ΐ)ΘΜΚσ20ΧλΟΩΧλΒΡΦέΗώy2(‘≠/Φΰ)”κt ±Φδ(Χλ)ΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚy2=ΓΣ
t+25(1ΓήtΓή20«“tΈΣ’ϊ ΐ)ΘΜΚσ20ΧλΟΩΧλΒΡΦέΗώy2(‘≠/Φΰ)”κt ±Φδ(Χλ)ΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚy2=ΓΣ![]() t+40(21ΓήtΓή40«“tΈΣ’ϊ ΐ).œ¬ΟφΈ“Ο«ά¥―–ΨΩ ’β÷÷…ΧΤΖΒΡ”–ΙΊΈ Χβ.
t+40(21ΓήtΓή40«“tΈΣ’ϊ ΐ).œ¬ΟφΈ“Ο«ά¥―–ΨΩ ’β÷÷…ΧΤΖΒΡ”–ΙΊΈ Χβ.
(1)»œ’φΖ÷Έω…œ±μ÷–ΒΡ ΐΝΩΙΊœΒΘ§άϊ”Ο―ßΙΐΒΡ“Μ¥ΈΚ· ΐΓΔΕΰ¥ΈΚ· ΐ ΓΔΖ¥±»άΐΚ· ΐΒΡ÷Σ Ε»ΖΕ®“ΜΗω¬ζΉψ’β–© ΐΨί÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
(2)«κ‘Λ≤βΈ¥ά¥40Χλ÷–Ρ«“ΜΧλΒΡœζ έάϊ»σΉν¥σΘ§Ήν¥σ»’œζ έάϊ»σ «Εύ…ΌΘΩ
(3)‘Ύ ΒΦ œζ έΒΡ«Α20Χλ÷–ΗΟΙΪΥΨΨωΕ®ΟΩœζ έ“ΜΦΰ…ΧΤΖΨΆΨη‘υa‘Σάϊ»σ(aΘΦ4)ΗχœΘΆϊΙΛ≥ΧΘ§ΙΪΥΨΆ®Ιΐœζ έΦ«¬ΦΖΔœ÷Θ§«Α20Χλ÷–Θ§ΟΩΧλΩέ≥ΐΨη‘υΚσΒΡ»’œζ έάϊ»σΥφ ±ΦδtΒΡ‘ω¥σΕχ‘ω¥σΘ§«σaΒΡ»Γ÷ΒΖΕΈß.
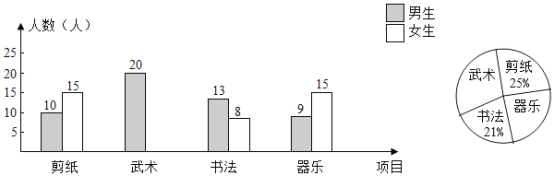
ΓΨΧβΡΩΓΩΈΣΝΥ’ΤΈ’ΑΥΡξΦΕ ΐ―ßΩΦ ‘ΨμΒΡΟϋΧβ÷ ΝΩ”κΡ―Ε»œΒ ΐΘ§ΟϋΧβΉιΫΧ ΠΗΑΆβΒΊ―ûÓΜΗωΥ°ΤΫœύΒ±ΒΡΑΥΡξΦΕΑύΦΕΫχ––‘Λ≤βΘ§ΫΪΩΦ ‘≥…Φ®Ζ÷≤Φ«ιΩωΫχ––¥ΠάμΖ÷ΈωΘ§÷Τ≥…ΤΒ ΐΖ÷≤Φ±μ»γœ¬(≥…Φ®ΒΟΖ÷ΨυΈΣ’ϊ ΐ)ΘΚ
Ήι±π | ≥…Φ®Ζ÷Ήι | ΤΒ ΐΤΒ¬ | ΤΒ ΐ |
1 |
| 2 | 0.05 |
2 |
| 4 | 0.10 |
3 |
|
| 0.2 |
4 |
| 10 | 0.25 |
5 |
|
|
|
6 |
| 6 | 0.15 |
ΚœΦΤ | 40 | 1.00 |
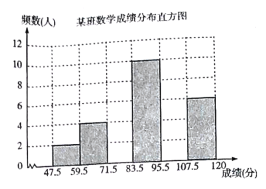
ΗυΨί±μ÷–ΧαΙ©ΒΡ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©ΤΒ ΐΖ÷≤Φ±μ÷–ΒΡ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΘΜ
ΘΜ
Θ®2Θ©“―÷Σ»Ϊ«χΑΥΡξΦΕΙ≤”–200ΗωΑύ(ΤΫΨυΟΩΑύ40»Υ)Θ§”Ο’βΖί ‘ΨμΦλ≤βΘ§108Ζ÷ΦΑ“‘…œΈΣ”≈–ψΘ§‘ΛΦΤ”≈–ψΒΡ»Υ ΐ‘ΦΈΣ Θ§72Ζ÷ΦΑ“‘…œΈΣΦΑΗώΘ§‘ΛΦΤΦΑΗώΒΡ»Υ ΐ‘ΦΈΣ Θ§ΦΑΗώΒΡΑΌΖ÷±»‘ΦΈΣ ΘΜ
Θ®3Θ©≤Ι≥δΆξ’ϊΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦ.