题目内容
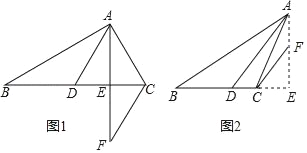
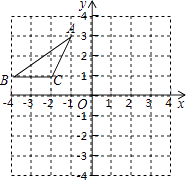
【题目】如图,在△ABC中,∠ABC=2∠C,AD平分∠BAC,求证:AB+BD=AC.

【答案】证明见解析
【解析】
在AC上截取AE=AB,利用“边角边”证明△ABD和△AED全等,根据全等三角形对应边相等可得DE=BD,全等三角形对应角相等可得∠AED=∠ABC,然后求出∠C=∠CDE,根据等角对等边可得CE=DE,然后结合图形整理即可得证.
如图,在AC上截取AE=AB,
∵AD平分∠BAC,
∴∠CAD=∠BAD,
在△ABD和△AED中,
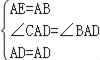 ,
,
∴△ABD≌△AED(SAS),
∴DE=BD,∠AED=∠ABC,
∵∠AED=∠C+∠CDE,∠ABC=2∠C,
∴∠CDE=∠C,
∴CE=DE,
∵AE+CE=AC,
∴AB+BD=AC.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
【题目】为了解学生的体能情况,随机选取了1000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
项目 | 长跑 | 短跑 | 跳绳 | 跳远 |
200 | √ | × | √ | √ |
300 | × | √ | × | √ |
150 | √ | √ | √ | × |
200 | √ | × | √ | × |
150 | √ | × | × | × |
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大?
【题目】某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 40 | 60 | 100 |
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E,F的人数分别为80,70
D.喜欢选修课C的人数最少