题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒 ![]() cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
【答案】
(1)
解:∵在Rt△ABC中,∠ACB=90°,AC=5,∠BAC=60°,
∴∠B=30°,
∴AB=2AC=10,BC=5 ![]() .
.
由题意知:BM=2t,CN= ![]() t,
t,
∴BN=5 ![]() -
- ![]() t,
t,
∵BM=BN,
∴2t=5 ![]() -
- ![]() t
t
解得: ![]() .
.
(2)
解:分两种情况:①当△MBN∽△ABC时,
则 ![]() ,即
,即 ![]() ,
,
解得:t= ![]() .
.
②当△NBM∽△ABC时,
则 ![]() ,即
,即 ![]() ,
,
解得:t= ![]() .
.
综上所述:当t= ![]() 或t=
或t= ![]() 时,△MBN与△ABC相似.
时,△MBN与△ABC相似.
(3)
解:过M作MD⊥BC于点D,则MD∥AC,
∴△BMD∽△BAC,
∴ ![]() ,
,
即 ![]() ,
,
解得:MD=t.
设四边形ACNM的面积为y,
∴y= ![]() =
= ![]() =
= ![]() .
.
∴根据二次函数的性质可知,当t= ![]() 时,y的值最小.
时,y的值最小.
此时, ![]() .
.
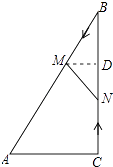
【解析】(1)由已知条件得出AB=10,BC=5 ![]() . 由题意知:BM=2t,CN=
. 由题意知:BM=2t,CN= ![]() t,BN=5
t,BN=5 ![]() -
- ![]() t,由BM=BN得出方程2t=5
t,由BM=BN得出方程2t=5 ![]() -
- ![]() t,解方程即可;(2)分两种情况:①当△MBN∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;②当△NBM∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;(3)过M作MD⊥BC于点D,则MD∥AC,证出△BMD∽△BAC,得出比例式求出MD=t.四边形ACNM的面积y=△ABC的面积﹣△BMN的面积,得出y是t的二次函数,由二次函数的性质即可得出结果.
t,解方程即可;(2)分两种情况:①当△MBN∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;②当△NBM∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;(3)过M作MD⊥BC于点D,则MD∥AC,证出△BMD∽△BAC,得出比例式求出MD=t.四边形ACNM的面积y=△ABC的面积﹣△BMN的面积,得出y是t的二次函数,由二次函数的性质即可得出结果.

 阅读快车系列答案
阅读快车系列答案【题目】林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的棵数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
成活的棵数m | 865 | 1356 | 2220 | 3500 | 7056 | 13170 | 17580 | 26430 |
成活的频率 | 0.865 | 0.904 | 0.888 | 0.875 | 0.882 | 0.878 | 0.879 | 0.881 |
估计该种幼树在此条件下移植成活的概率为 .