题目内容
【题目】自主学习，请阅读下列解题过程．
解一元二次不等式：x2﹣5x＞0．
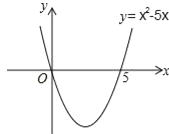
解：设x2﹣5x=0，解得：x1=0，x2=5，则抛物线y=x2﹣5x与x轴的交点坐标为（0，0）和（5，0）．画出二次函数y=x2﹣5x的大致图象（如图所示），由图象可知：当x＜0，或x＞5时函数图象位于x轴上方，此时y＞0，即x2﹣5x＞0，所以，一元二次不等式x2﹣5x＞0的解集为：x＜0或x＞5．
通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：
（1）上述解题过程中，渗透了下列数学思想中的 和 ．（只填序号）
①转化思想 ②分类讨论思想 ③数形结合思想
（2）一元二次不等式x2﹣5x＜0的解集为 ．
（3）用类似的方法写出一元二次不等式的解集：x2﹣2x﹣3＞0． ．
【答案】（1）①，③（2）0＜x＜5（3）x＜﹣1或x＞3
【解析】
试题分析：（1）上述解题过程中，渗透了下列数学思想中的①和③；
故答案为：①，③；
（2）由图象可知：当0＜x＜5时函数图象位于x轴下方，
此时y＜0，即x2﹣5x＜0，
∴一元二次不等式x2﹣5x＜0的解集为：0＜x＜5；
故答案为：0＜x＜5．
（3）设x2﹣2x﹣3=0，
解得：x1=3，x2=﹣1，
∴抛物线y=x2﹣2x﹣3与x轴的交点坐标为（3，0）和（﹣1，0）．
画出二次函数y=x2﹣2x﹣3的大致图象（如图所示），
由图象可知：当x＜﹣1，或x＞3时函数图象位于x轴上方，
此时y＞0，即x2﹣2x﹣3＞0，
∴一元二次不等式x2﹣2x﹣3＞0的解集为：x＜﹣1或x＞3．
故答案为x＜﹣1或x＞3
练习册系列答案
相关题目
