Question

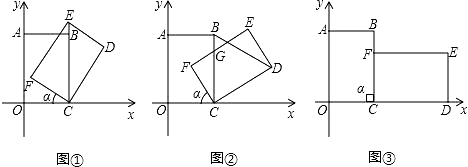
【题目】把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中，将它绕点C顺时针旋转a角，旋转后的矩形记为矩形EDCF．在旋转过程中，

（1）如图①，当点E在射线CB上时，E点坐标为 ；

（2）当△CBD是等边三角形时，旋转角a的度数是 （a为锐角时）；

（3）如图②，设EF与BC交于点G，当EG=CG时，求点G的坐标；

（4）如图③，当旋转角a=90°时，请判断矩形EDCF的对称中心H是否在以C为顶点，且经过点A的抛物线上．

Answer 1

【答案】（1）E（4，2）（2）60°（3）（4）点H不在此抛物线上

【解析】

试题分析：（1）依题意得点E在射线CB上，横坐标为4，纵坐标根据勾股定理可得点E．

（2）已知∠BCD=60°，∠BCF=30°，然后可得∠α=60°．

（3）设CG=x，则EG=x，FG=6﹣x，根据勾股定理求出CG的值．

（4）设以C为顶点的抛物线的解析式为y=a（x﹣4）2，把点A的坐标代入求出a值．当x=7时代入函数解析式可得解．

试题解析：（1）E（4，2）

（2）60°

（3）设CG=x，则EG=x，FG=6﹣x，

在Rt△FGC中，∵CF2+FG2=CG2，

∴42+（6﹣x）2=x2

解得，

即

∴

（4）设以C为顶点的抛物线的解析式为y=a（x﹣4）2，

把A（0，6）代入，得6=a（0﹣4）2．

解得a=．

∴抛物线的解析式为y=（x﹣4）2

∵矩形EDCF的对称中心H即为对角线FD、CE的交点，

∴H（7，2）．

当x=7时，

∴点H不在此抛物线上．