题目内容
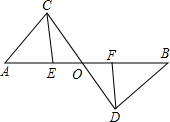 如图,已知AB、CD相交于O点,△AOC≌△BOD,E、F分别在OA、OB上,要使△EOC≌△FOD,添加的一个条件不可以是
如图,已知AB、CD相交于O点,△AOC≌△BOD,E、F分别在OA、OB上,要使△EOC≌△FOD,添加的一个条件不可以是
- A.CE=DF
- B.∠CEA=∠DFB
- C.∠OCE=∠ODF
- D.OE=OF
A
分析:因为△AOC≌△BOD,所以要使△EOC≌△FOD,隐含的已知条件是:∠COE=∠DOF,CO=OD;据三角形的判定方法ASA、AAS、SAS,添加条件去判断即可.
解答:∵△AOC≌△BOD,
∴CO=OD,
又∵∠COE=∠DOF(对顶角相等),
∴要使△EOC≌△FOD,则添加的一个条件是∠CEA=∠DFB,即说明其补角是相等的,符合AAS;
或∠OCE=∠ODF,符合ASA;或OE=OF,符合SAS.A选项不符合判定定理,
故选A.
点评:本题考查了全等三角形的判定;解题的关键是牢记三角形的判定定理,并能熟练应用.从已知条件入手,结合全等的判定方法,通过分析推理,对选项一个个进行验证,做到由易到难,不重不漏.
分析:因为△AOC≌△BOD,所以要使△EOC≌△FOD,隐含的已知条件是:∠COE=∠DOF,CO=OD;据三角形的判定方法ASA、AAS、SAS,添加条件去判断即可.
解答:∵△AOC≌△BOD,
∴CO=OD,
又∵∠COE=∠DOF(对顶角相等),
∴要使△EOC≌△FOD,则添加的一个条件是∠CEA=∠DFB,即说明其补角是相等的,符合AAS;
或∠OCE=∠ODF,符合ASA;或OE=OF,符合SAS.A选项不符合判定定理,
故选A.
点评:本题考查了全等三角形的判定;解题的关键是牢记三角形的判定定理,并能熟练应用.从已知条件入手,结合全等的判定方法,通过分析推理,对选项一个个进行验证,做到由易到难,不重不漏.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
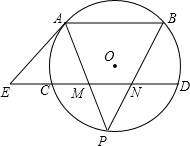 如图,已知AB、CD是⊙O的两条平行弦,过A点的⊙O的切线AE和DC的延长线交于E点,P为弧
如图,已知AB、CD是⊙O的两条平行弦,过A点的⊙O的切线AE和DC的延长线交于E点,P为弧
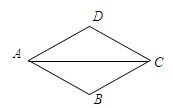 11、如图,已知AB=BC=CD=AD,∠DAC=40°,那么∠B=
11、如图,已知AB=BC=CD=AD,∠DAC=40°,那么∠B= 如图,已知AB,CD相交于点0,△ACO≌△BD0,CE∥DF,求证:CE=DF.
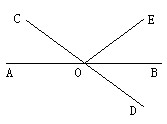
如图,已知AB,CD相交于点0,△ACO≌△BD0,CE∥DF,求证:CE=DF.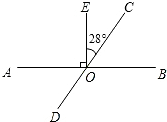 如图,已知AB、CD相交于点O,OE⊥AB,∠EOC=28°,则∠AOD=
如图,已知AB、CD相交于点O,OE⊥AB,∠EOC=28°,则∠AOD=